��Ŀ����
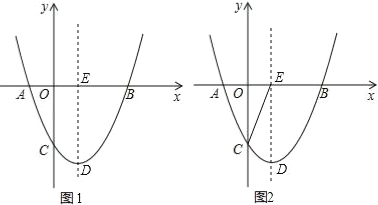
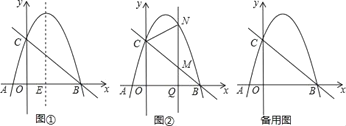
����Ŀ����ͼ����֪������y=ax2��3ax��4a(a��0)��ͼ����x�ύ��A��B����(A��B�����)����y�������ύ�ڵ�C������BC�����κ����ĶԳ�����x��Ľ���ΪE��
(1)�����ߵĶԳ�����x��Ľ���E����Ϊ_____����A������Ϊ_____��
(2)����EΪԲ�ĵ�Բ��y���ֱ��BC�����У�����������ߵĽ���ʽ��
(3)��(2)�������£���ͼ��Q(m��0)��x����������һ�㣬����Q��y���ƽ���ߣ���ֱ��BC���ڵ�M���������߽��ڵ�N������CN������CMN��CN���ۣ�M�Ķ�Ӧ��ΪM������ͼ����̽�����Ƿ���ڵ�Q��ʹ��M��ǡ������y���ϣ������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�(1)E(![]() ��0)��A(��1��0)��(2)y=
��0)��A(��1��0)��(2)y=![]() ��(3)���ڣ���Q����Ϊ(
��(3)���ڣ���Q����Ϊ(![]() ��0)��(
��0)��(![]() ��0)
��0)
��������
��1�����ݶԳ��ṫʽ���������E���꣬��y��0���ⷽ�̼��������A���꣮
��2����ͼ���У�����E��ֱ��BC�����ڵ�D������DE����DE��BC����tan��OBC��![]() ���г����̼��ɽ����
���г����̼��ɽ����
��3����������������N��ֱ��BC�Ϸ�������N��ֱ��BC�·����ֱ��г����̼��ɽ����
�⣺(1)���Գ���x=![]() ��
��
����E����(![]() ��0)��
��0)��
��y=0������ax2��3ax��4a=0��
��x=��1��4��
����A����(��1��0)��
�ʴ𰸷ֱ�Ϊ(![]() ��0)��(��1��0)��
��0)��(��1��0)��
(2)��ͼ���У�����E��ֱ��BC�����ڵ�D������DE����DE��BC��

��DE=OE=![]() ��EB=
��EB=![]() ��OC=��4a��
��OC=��4a��
��DB=![]() ��
��
��tan��OBC=![]() ��
��
��![]() �����a=
�����a=![]() ��
��
�������߽���ʽΪy=![]() ��
��
(3)��ͼ���У���������M��CN=��NCB��

��MN��OM����
���M��CN=��CNM��
��MN=CM��
����B������Ϊ(4��0)����C������Ϊ(0��3)��
�� ֱ��BC����ʽΪy=��![]() x+3��BC=5��
x+3��BC=5��
��M(m����![]() m+3)��N(m����
m+3)��N(m����![]() m2+
m2+![]() m+3)����MF��OC��F��
m+3)����MF��OC��F��
��sin��BCO=![]() ��
��
��![]() ��
��
��CM=![]() m��
m��
����N��ֱ��BC�Ϸ�ʱ����![]() m2+
m2+![]() m+3��(��
m+3��(��![]() m+3)=
m+3)=![]() m��
m��
��ã�m=![]() ��0(����)��
��0(����)��
��Q1(![]() ��0)��
��0)��
����N��ֱ��BC�·�ʱ��(��![]() m+3)��(��
m+3)��(��![]() m2+
m2+![]() m+3)=
m+3)=![]() m��
m��
���m=![]() ��0(����)��
��0(����)��
��Q2(![]() ��0)��
��0)��
������������Q����Ϊ(![]() ��0)��(
��0)��(![]() ��0)��
��0)��