题目内容
【题目】阅读解题过程,回答问题. 如图,OC在∠AOB内,∠AOB和∠COD都是直角,且∠BOC=30°,求∠AOD的度数.
解:过O点作射线OM,使点M,O,A在同一直线上.
因为∠MOD+∠BOD=90°,∠BOC+∠BOD=90°,
所以∠BOC=∠MOD,
所以∠AOD=180°﹣∠BOC=180°﹣30°=150°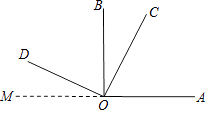
(1)如果∠BOC=60°,那么∠AOD等于多少度?如果∠BOC=n°,那么∠AOD等于多少度?
(2)如果∠AOB=∠DOC=x°,∠AOD=y°,求∠BOC的度数.
【答案】
(1)解:如果∠BOC=60°,那么∠AOD=180°﹣60°=120°
如果∠BOC=n°,那么∠AOD=180°﹣n°
(2)解:因为∠AOB=∠DOC=x°,∠AOD=y°,
且∠AOD=∠AOB+∠DOC﹣∠BOC
所以∠BOC=∠AOB+∠DOC﹣∠AOD
=2x°﹣y°
【解析】(1)根据题目中解答过程得出的结论,直接计算即可;(2)根据题目中解答过程得出的结论,用含x和y的式子表示出∠BOC的度数即可.
【考点精析】本题主要考查了余角和补角的特征的相关知识点,需要掌握互余、互补是指两个角的数量关系,与两个角的位置无关才能正确解答此题.

练习册系列答案
相关题目