题目内容
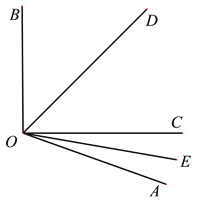
【题目】甲、乙两地距离300km,一辆货车和一辆轿车先后从甲地出发驶向乙地.如图,线段OA表示货车离甲地的距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系,根据图像,解答下列问题: 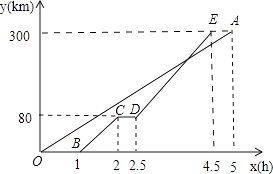
(1)线段CD表示轿车在中途停留了h;
(2)求轿车从甲地出发后经过多长时间追上货车.
【答案】
(1)0.5
(2)解:设过点D(2.5,80),点E(4.5,300)的直线解析式为:y=kx+b,
则 ![]()
解得, ![]()
∴过DE的直线解析式为:y=110x﹣195,
设过点O(0,0),A(5,300)的直线的解析式为y=mx,
则5m=300,得m=60,
即过点O、A的直线的解析式为:y=60x,
![]()
解得,x=3.9,
3.9﹣1=2.9h,
即轿车从甲地出发后经过2.9h追上货车
【解析】解:(1)由图像可知, 线段CD表示轿车在中途停留的时间是:2.5﹣2=0.5h,
故答案为:0.5;
(1)根据函数图像可以得到轿车在中途停留的时间;(2)由图像可知,两车相遇在轿车行驶的DE段,只要求出直线DE的解析式和直线OA的解析式,联立方程组即可求得相遇时间,用相遇的时间﹣轿车晚行驶的1小时,即可求得轿车从甲地出发后经过多长时间追上货车.

练习册系列答案
相关题目