题目内容
【题目】已知某开发区有一块四边形的空地ABCD,如图所示,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,求这块空地的面积? 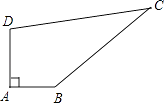
【答案】解:连接BD,如图所示: 在Rt△ABD中,BD2=AB2+AD2=32+42=52 ,
在△CBD中,CD2=132BC2=122 ,
而122+52=132 ,
即BC2+BD2=CD2 ,
∴∠DBC=90°,
S四边形ABCD=S△BAD+S△DBC= ![]() ABAD+
ABAD+ ![]() BDBC=36m2;
BDBC=36m2;
答:这块空地的面积为36m2 . 
【解析】仔细分析题目,需要求得四边形的面积才能求得结果.连接BD,在直角三角形ABD中可求得BD的长,由BD、CD、BC的长度关系可得三角形DBC为一直角三角形,DC为斜边;由此看,四边形ABCD由Rt△ABD和Rt△DBC构成,则容易求解.

练习册系列答案
相关题目