题目内容
【题目】已知∠AOB=120°,∠COD=60°,OE平分∠BOC
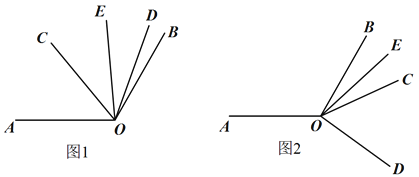
(1)如图1.当∠COD在∠AOB的内部时
①若∠AOC=39°40′,求∠DOE的度数;
②若∠AOC=α,求∠DOE的度数(用含α的代数式表示),
(2)如图2,当∠COD在∠AOB的外部时,(1)中∠AOC与∠DOE的数量关系还成立吗?若成立,请推导出∠AOC与∠DOE的度数之间的关系;若不成立,请说明理由.
【答案】(1)①19°50′;②![]() α;(2)∠AOC=2∠DOE的关系成立;理由见解析.
α;(2)∠AOC=2∠DOE的关系成立;理由见解析.
【解析】
(1)①由∠AOB=120°,∠COD=60°得∠BOC=80°20′,根据角平分线得∠DOE=19°50′;
②方法同上,见详解,
(2)根据题意得∠AOC=120°+∠BOC,利用角平分线得∠DOE=60°+![]() ∠BOC,即可解题.
∠BOC,即可解题.
解:(1)①∵∠AOB=120°,∠COD=60°,∠AOC=39°40′,
∴∠BOC=∠AOB﹣∠AOC=120°﹣39°40′=80°20′,
∵OE平分∠BOC,
∴∠COE=![]() ∠BOC=40°10′,
∠BOC=40°10′,
∴∠DOE=∠COD﹣∠COE=19°50′;
②∵∠AOB=120°,∠COD=60°,∠AOC=α,
∴∠BOC=∠AOB﹣∠AOC=120°﹣α,
∵OE平分∠BOC,
∴∠COE=![]() ∠BOC=60°﹣
∠BOC=60°﹣![]() α,
α,
∴∠DOE=![]() α;
α;
(2)(1)中∠AOC=2∠DOE的关系成立;
理由是:∵∠AOC=120°+∠BOC,∠DOE=60°+∠COE,
∵OE平分∠BOC,
∴∠COE=![]() ∠BOC,
∠BOC,
∴∠DOE=60°+![]() ∠BOC
∠BOC
∴2∠DOE=120°+∠BOC
∴∠AOC=2∠DOE;

 阅读快车系列答案
阅读快车系列答案【题目】某电脑店有A、B两种型号的打印机和C、D、E三种芯片出售.每种型号的打印机均需要一种芯片配套才能打印.
(1)下列是该店用树形图或列表设计的配套方案,①的位置应填写 , ②的位置应 填写
(2)若仅有B型打印机与E种芯片不配套,则上面(1)中的方案配套成功率是
芯片 | C | D | E |
A | (A,C) | (A,D) | ② |
B | (B,C) | (B,D) | (B,E) |