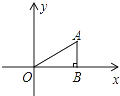��Ŀ����
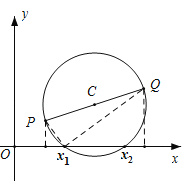
����Ŀ����2017�㽭ʡ̨���У���ƽ��ֱ������ϵ�У�����ֱ�����ǰ�����ҵ�һԪ���η��̵�ʵ������������ڷ���![]() �����������ǣ�
�����������ǣ�
��һ�������ݷ��̵�ϵ��������ȷ��һ�Թ̶���A��0��1����B��5��2����
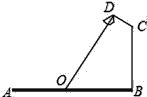
�ڶ�����������ƽ�����ƶ�һ��ֱ�����ǰ壬ʹһ��ֱ�DZߺ����A����һ��ֱ�DZߺ����B��
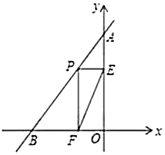
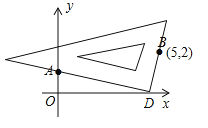
�����������ƶ������У������ǰ��ֱ�Ƕ�������x���ϵ�C��ʱ����C�ĺ�����m��Ϊ�÷��̵�һ��ʵ��������ͼ1����
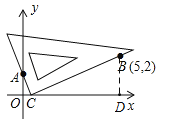
���IJ����������ǰ�ֱ�Ƕ����λ�ã���������x������һ��D��ʱ����D�ĺ�����n��Ϊ�÷��̵���һ��ʵ������
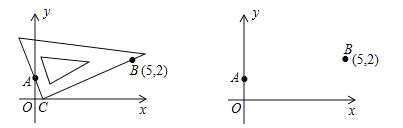
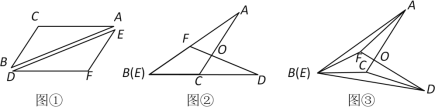
��1����ͼ2�У����������IJ����IJ�������������D���뱣��������Dʱֱ�����ǰ�����ֱ�DZߵĺۼ�����
��2�����ͼ1����֤�����������������õ���m���Ƿ���![]() ��һ��ʵ������
��һ��ʵ������
��3�����������Ĺؼ���ȷ�������̶����λ�ã���Ҫ�Դ˷����ҵ�һԪ���η���![]() ��a��0��
��a��0��![]() ��0����ʵ����������ֱ��д��һ�Թ̶�������ꣻ
��0����ʵ����������ֱ��д��һ�Թ̶�������ꣻ
��4��ʵ���ϣ���3���еĹ̶����������ԣ�һ��أ���m1��n1��m2��n2��a��b��c֮�����������Ĺ�ϵʱ����P��m1��n1����Q��m2��n2�����Ƿ���Ҫ���һ�Թ̶��㣿
���𰸡���1����ͼ����������2��֤������������3��A��0��1����B����![]() ��
��![]() ����A��0��
����A��0��![]() ����B����
����B����![]() ��c���ȣ���4��
��c���ȣ���4��![]() ��
��![]() =
=![]() ��
��
�����������⣨1�����������IJ����IJ�������������D���ɣ�
��2������B��BD��x���ڵ�D��������AOC�ס�CDB���ɵ�![]() �������ó�
�������ó�![]() ����
����![]() ���ݴ˿ɵ�m�Ƿ���
���ݴ˿ɵ�m�Ƿ���![]() ��ʵ������
��ʵ������
��3������![]() ��a��0���ɻ�Ϊ
��a��0���ɻ�Ϊ![]() ��ģ���о�С�������ɵ�һ�Թ̶�������ꣻ
��ģ���о�С�������ɵ�һ�Թ̶�������ꣻ
��4�����跽�̵ĸ�Ϊx���������������ƿɵ�![]() �������õ�
�������õ�![]() ���ٸ���
���ٸ���![]() ���ɵ�
���ɵ�![]() �����Ƚ�ϵ���ɵ�m1��n1��m2��n2��a��b��c֮��Ĺ�ϵ��
�����Ƚ�ϵ���ɵ�m1��n1��m2��n2��a��b��c֮��Ĺ�ϵ��
�����������1����ͼ��ʾ����D��Ϊ����
��2����ͼ��ʾ������B��BD��x���ڵ�D��������AOC=��CDB=90������ACO=��CBD���ɵ���AOC�ס�CDB����![]() ����
����![]() ����m��5��m��=2����
����m��5��m��=2����![]() ����m�Ƿ���
����m�Ƿ���![]() ��ʵ������
��ʵ������
��3������![]() ��a��0���ɻ�Ϊ
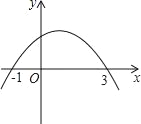
��a��0���ɻ�Ϊ![]() ��ģ���о�С�������ɵã�A��0��1����B����
��ģ���о�С�������ɵã�A��0��1����B����![]() ��
��![]() ����A��0��
����A��0��![]() ����B����
����B����![]() ��c���ȣ�
��c���ȣ�
��4����ͼ��P��m1��n1����Q��m2��n2�����跽�̵ĸ�Ϊx���������������ƿɵ�![]() ����ʽ�ɻ�Ϊ
����ʽ�ɻ�Ϊ![]() ������
������![]() ����
����![]() �����Ƚ�ϵ���ɵ�
�����Ƚ�ϵ���ɵ�![]() ��
��![]() =
=![]() ��
��