题目内容
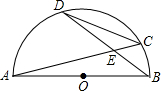 如图,半圆O的直径AB=7,两弦AC、BD相交于点E,弦CD=
如图,半圆O的直径AB=7,两弦AC、BD相交于点E,弦CD=| 7 |
| 2 |
A、2
| ||
B、4
| ||
C、
| ||
D、
|
分析:根据圆周角定理得出的两组相等的对应角,易证得△AEB∽△DEC,根据CD、AB的长,即可求出两个三角形的相似比;设BE=x,则DE=5-x,然后根据相似比表示出AE、EC的长,连接BC,首先在Rt△BEC中,根据勾股定理求得BC的表达式,然后在Rt△ABC中,由勾股定理求得x的值,进而可求出DE的长.
解答: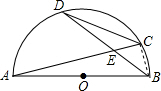 解法一:
解法一:
∵∠D=∠A,∠DCA=∠ABD,
∴△AEB∽△DEC;
∴
=
=
=
;
设BE=2x,则DE=5-2x,EC=x,AE=2(5-2x);
连接BC,则∠ACB=90°;
Rt△BCE中,BE=2x,EC=x,则BC=
x;
在Rt△ABC中,AC=AE+EC=10-3x,BC=
x;
由勾股定理,得:AB2=AC2+BC2,
即:72=(10-3x)2+(
x)2,
整理,得4x2-20x+17=0,解得x1=
+
,x2=
-
;
由于x<
,故x=
-
;
则DE=5-2x=2
.
解法二:连接OD,OC,AD,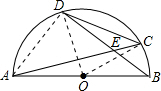
∵OD=CD=OC
则∠DOC=60°,∠DAC=30°
又AB=7,BD=5,
∴AD=2
,
在Rt△ADE中,∠DAC=30°,
所以DE=2
.
故选A.
 解法一:
解法一:∵∠D=∠A,∠DCA=∠ABD,
∴△AEB∽△DEC;
∴
| EC |
| BE |
| DE |
| AE |
| CD |
| AB |
| 1 |
| 2 |
设BE=2x,则DE=5-2x,EC=x,AE=2(5-2x);
连接BC,则∠ACB=90°;
Rt△BCE中,BE=2x,EC=x,则BC=
| 3 |
在Rt△ABC中,AC=AE+EC=10-3x,BC=
| 3 |
由勾股定理,得:AB2=AC2+BC2,
即:72=(10-3x)2+(
| 3 |
整理,得4x2-20x+17=0,解得x1=
| 5 |
| 2 |
| 2 |
| 5 |
| 2 |
| 2 |
由于x<
| 10 |
| 3 |
| 5 |
| 2 |
| 2 |
则DE=5-2x=2
| 2 |
解法二:连接OD,OC,AD,

∵OD=CD=OC
则∠DOC=60°,∠DAC=30°
又AB=7,BD=5,
∴AD=2
| 6 |
在Rt△ADE中,∠DAC=30°,
所以DE=2
| 2 |
故选A.
点评:此题主要考查了圆周角定理、相似三角形的判定和性质、勾股定理的应用等知识;本题要特别注意的是BE、DE不是相似三角形的对应边,它们的比不等于相似比,以免造成错解.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
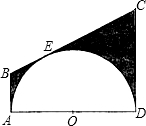 如图,半圆O的直径AD=12cm,AB,BC,CD分别与半圆O切于点A,E,D.
如图,半圆O的直径AD=12cm,AB,BC,CD分别与半圆O切于点A,E,D.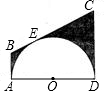 如图,半圆O的直径AD=12cm,AB、BC、CD分别与半圆O切于点A、E、D.
如图,半圆O的直径AD=12cm,AB、BC、CD分别与半圆O切于点A、E、D.
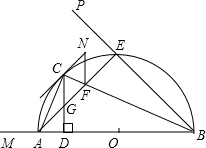 N∥CD,过C作圆的切线交FN于N.
N∥CD,过C作圆的切线交FN于N. 如图,半圆O的直径为6cm,∠BAC=30°,则阴影部分的面积是( )
如图,半圆O的直径为6cm,∠BAC=30°,则阴影部分的面积是( ) 如图,半圆O的直径AB=20,将半圆O绕点B顺针旋转45°得到半圆O′,与AB交于点P.
如图,半圆O的直径AB=20,将半圆O绕点B顺针旋转45°得到半圆O′,与AB交于点P.