Question

如图，半圆O的直径为6cm，∠BAC=30°，则阴影部分的面积是（　　）

• A．(12π-9

  3

  ) cm2
• B．(3π-

  9

  4

  ) cm2
• C．(3π-

  9

  2

  3

  ) cm2
• D．(3π-

  9

  4

  3

  ) cm2

Answer 1

分析：如图，连接OC．图中阴影部分的面积=半圆的面积-△AOC的面积-扇形CBO的面积．

解答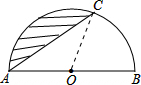：解：如图，连接OC．
∵半圆O的直径为6cm，∠BAC=30°，
∴OA=OC=OB=3cm，∠COB=2∠BAC=60°，
∴S_△AOC=

1

2

OA•OC•sin120°=

1

2

×3×3×

3

2

=

9 3

4

（cm²）．
S_扇形OBC=

60π×32

360

=

3π

2

（cm²）．
∴S_阴影=

1

2

π×3²-S_△AOC-S_扇形OBC=3π-

9 3

4

（cm²）．
故选：D．

点评：本题考查了扇形的面积计算．解题时，利用了“分割法”求得阴影部分的面积．