题目内容
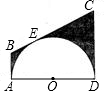 如图,半圆O的直径AD=12cm,AB、BC、CD分别与半圆O切于点A、E、D.
如图,半圆O的直径AD=12cm,AB、BC、CD分别与半圆O切于点A、E、D.(1)线段AB、CD与BC之间有什么关系?并说明理由;
(2)设AB=x,CD=y,求y与x之间的函数关系式;
(3)如果AB=4,求图中阴影部分的面积.
分析:(1)由CB、BA和CD都是半圆O的切线,由切线长定理得:CE=CD,BE=BA,所以:AB+CD=BC;
(2)过点B作BF⊥CD于F,由BA、CD是半圆O的切线,AD是半圆O的直径,可得BA⊥AD,CD⊥AD,故BF=AD=12,DF=AB=x;在Rt△CFB中,BC2=BF2+FC2,可得出y与x之间的函数关系式;
(3)因为AB=4,代入函数关系式可得出y的值,由x、y可得出梯形和半圆的面积,由S阴=S梯-S半圆可得出阴影部分的面积.
(2)过点B作BF⊥CD于F,由BA、CD是半圆O的切线,AD是半圆O的直径,可得BA⊥AD,CD⊥AD,故BF=AD=12,DF=AB=x;在Rt△CFB中,BC2=BF2+FC2,可得出y与x之间的函数关系式;
(3)因为AB=4,代入函数关系式可得出y的值,由x、y可得出梯形和半圆的面积,由S阴=S梯-S半圆可得出阴影部分的面积.
解答:解:(1)AB+CD=BC.
∵CB、BA和CD都是半圆O的切线
由切线长定理得:
CE=CD,BE=BA
∴AB+CD=BC
(2)过点B作BF⊥CD于F,如图所示:
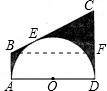
∵BA、CD是半圆O的切线,AD是半圆O的直径,
∴BA⊥AD,CD⊥AD,
∴四边形ABFD是矩形,
∴BF=AD=12,DF=AB=x,
∴CF=CD-DF=y-x;
∵BC=AB+CD=x+y,
在Rt△CFB中,BF2+CF2=BC2,
∴122+(y-x)2=(y+x)2,
∴y与x之间的函数关系式为:
y=
(x>0).
(3)当AB=4时,即x=4,则y=
=
=9,
∴CD=9cm,
∵S半圆=
π×OA2=
π×62=18πcm2,S梯形ABCD=
(AB+CD)×AD=
(4+9)•12=78cm2;
∴S阴=S梯-S半圆=(78-18π)cm2.
∵CB、BA和CD都是半圆O的切线
由切线长定理得:
CE=CD,BE=BA
∴AB+CD=BC
(2)过点B作BF⊥CD于F,如图所示:

∵BA、CD是半圆O的切线,AD是半圆O的直径,
∴BA⊥AD,CD⊥AD,
∴四边形ABFD是矩形,
∴BF=AD=12,DF=AB=x,
∴CF=CD-DF=y-x;
∵BC=AB+CD=x+y,
在Rt△CFB中,BF2+CF2=BC2,
∴122+(y-x)2=(y+x)2,
∴y与x之间的函数关系式为:
y=
| 36 |
| x |
(3)当AB=4时,即x=4,则y=
| 36 |
| x |
| 36 |
| 4 |
∴CD=9cm,
∵S半圆=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S阴=S梯-S半圆=(78-18π)cm2.
点评:本题考查了切线的性质,梯形的面积,勾股定理的应用.

练习册系列答案
相关题目
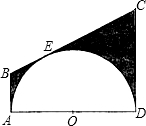 如图,半圆O的直径AD=12cm,AB,BC,CD分别与半圆O切于点A,E,D.
如图,半圆O的直径AD=12cm,AB,BC,CD分别与半圆O切于点A,E,D.
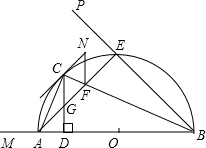 N∥CD,过C作圆的切线交FN于N.
N∥CD,过C作圆的切线交FN于N. 如图,半圆O的直径为6cm,∠BAC=30°,则阴影部分的面积是( )
如图,半圆O的直径为6cm,∠BAC=30°,则阴影部分的面积是( ) 如图,半圆O的直径AB=20,将半圆O绕点B顺针旋转45°得到半圆O′,与AB交于点P.
如图,半圆O的直径AB=20,将半圆O绕点B顺针旋转45°得到半圆O′,与AB交于点P.