题目内容
【题目】．附图（①）为一张三角形ABC纸片，P点在BC上．今将A折至P时，出现折线BD，其中D点在AC上，如图（②）所示．若△ABC的面积为80，△DBC的面积为50，则BP与PC的长度比为何？（ ）
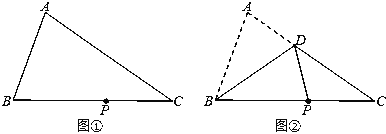
A．3：2 B．5：3 C．8：5 D．13：8
【答案】A．
【解析】
试题 本题考查了折叠的性质：折叠前后的两个三角形是全等三角形，它们的面积相等．由题意分别计算出△DBP与△DCP的面积，从而BP：PC=S△DBP：S△DCP，问题可解．
解：由题意可得：S△ABD=S△ABC﹣S△DBC=80﹣50=30．
由折叠性质可知，S△DBP=S△ABD=30，
∴S△DCP=S△DBC﹣S△DBP=50﹣30=20．
∴BP：PC=S△DBP：S△DCP=30：20=3：2．
故选A．
练习册系列答案
优百分课时互动系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
相关题目
【题目】某面粉加工厂加工的面粉，用每袋可装10g面粉的袋子装了200袋经过称重，质量超过标准质量10kg的用正数表示，质量低于标准质量10kg的用负数表示，结果记录如下
与标准质量的偏差(kg) | ﹣1.5 | ﹣1 | ﹣0.5 | 0 | 0.5 | 1 | 2 |
袋数(袋) | 40 | 30 | 10 | 25 | 40 | 20 | 35 |
(1)求这批面粉的总质量；
(2)如果100kg小麦加工80kg面粉，那么这批面粉是由多少千克小麦加工的？
