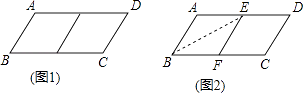ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃКЪ§жсЩЯгаAЁЂBСНЕуЃЌЗжБ№ЖдгІЕФЪ§ЮЊaЃЌbЃЌвбжЊЃЈa+1ЃЉ2гы|bЉ3|ЛЅЮЊЯрЗДЪ§ЃЎЕуPЮЊЪ§жсЩЯвЛЖЏЕуЃЌЖдгІЮЊxЃЎ
ЃЈ1ЃЉa=ЁЁЁЁЃЛb=ЁЁ ЁЁ
ЃЈ2ЃЉШєЕуPЕНЕуAКЭЕуBЕФОрРыЯрЕШЃЌдђЕуPЖдгІЕФЪ§ЪЧЁЁ ЁЁ
ЃЈ3ЃЉЪ§жсЩЯЪЧЗёДцдкЕуPЃЌЪЙЕуPЕНЕуAКЭЕуBЕФОрРыжЎКЭЮЊ5ЃПШєДцдкЃЌЧыЧѓГіxЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЛ
ЃЈ4ЃЉ|xЉa|+|xЉb|ЕФзюаЁжЕ=ЁЁ ЁЁ
ЃЈ5ЃЉЕБЕуPвдУПЗжжг1ИіЕЅЮЛГЄЖШЕФЫйЖШДгOЕуЯђзѓдЫЖЏЃЌЕуAвдУПЗжжг5ИіЕЅЮЛГЄЖШЯђзѓдЫЖЏЃЌЮЪМИЗжжгЪБЕуPЕНЕуAЁЂЕуBЕФОрРыЯрЕШЃП
ЁОД№АИЁП(1) Љ1ЃЌ3ЃЛ(2)1;(3) x1=Љ1.5ЃЌx2=3.5ЃЛ(4)4;(5) ![]() ЗжжгЪБЕуPЕНЕуAЁЂЕуBЕФОрРыЯрЕШ
ЗжжгЪБЕуPЕНЕуAЁЂЕуBЕФОрРыЯрЕШ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЃЈa+1ЃЉ2гы|b-3|ЛЅЮЊЯрЗДЪ§ЃЌПЩвдЧѓЕУaЁЂbЕФжЕЃЛ
ЃЈ2ЃЉИљОнЬтвтПЩвдЕУЕНЙигкxЕФЗНГЬЃЌДгЖјПЩвдЧѓЕУxЕФжЕЃЛ
ЃЈ3ЃЉИљОнЬтвтПЩвдСаГіЙигкxЕФЗНГЬЃЌБОЬтЕУвдНтОіЃЛ
ЃЈ4ЃЉИљОнЬтвтЃЌРћгУЗжРрЬжТлЕФЫМЯыПЩвдНтД№БОЬтЃЛ
ЃЈ5ЃЉИљОнЬтвтПЩвдСаГіЯргІЕФЗНГЬЃЌБОЬтЕУвдНтОі.
Нт:ЃЈ1ЃЉЁпЃЈa+1ЃЉ2гы|bЉ3|ЛЅЮЊЯрЗДЪ§ЃЌ
Ёрa+1=0ЃЌbЉ3=0ЃЌ
НтЕУЃЌa=Љ1ЃЌb=3ЃЌ
ЙЪД№АИЮЊЃКЉ1ЃЌ3ЃЛ
ЃЈ2ЃЉгЩЬтвтПЩЕУЃЌ
|xЉЃЈЉ1ЃЉ|=|xЉ3|ЃЌ
НтЕУЃЌx=1ЃЌ
ЙЪД№АИЮЊЃК1ЃЛ
ЃЈ3ЃЉЪ§жсЩЯДцдкЕуPЃЌЪЙЕуPЕНЕуAКЭЕуBЕФОрРыжЎКЭЮЊ5ЃЌ
гЩЬтвтПЩЕУЃЌ
|xЉЃЈЉ1ЃЉ|+|xЉ3|=5ЃЌ
НтЕУЃЌx1=Љ1.5ЃЌx2=3.5ЃЛ
ЃЈ4ЃЉЁпa=Љ1ЃЌb=3ЃЌ
Ёр|xЉa|+|xЉb|=|xЉЃЈЉ1ЃЉ|+|xЉ3|=|x+1|+|xЉ3|ЃЌ
ЕБxЃО3ЪБЃЌ|x+1|+|xЉ3|=x+1+xЉ3=2xЉ2ЃО4ЃЌ
ЕБЉ1ЁмxЁм3ЪБЃЌ|x+1|+|xЉ3|=x+1+3Љx=4ЃЌ
ЕБxЃМЉ1ЪБЃЌ|x+1|+|xЉ3|=ЉxЉ1+3Љx=Љ2x+2ЃО4ЃЌ
Ёр|x+1|+|xЉ3|ЕФзюаЁжЕЪЧ4ЃЌ
ЙЪД№АИЮЊЃК4ЃЛ
ЃЈ5ЃЉЩшtЗжжгЪБЕуPЕНЕуAЁЂЕуBЕФОрРыЯрЕШЃЌ
ЉtЉЃЈЉ1Љ5tЃЉ=t+3ЃЌ
НтЕУЃЌt=![]() ЃЌ
ЃЌ
Д№ЃК![]() ЗжжгЪБЕуPЕНЕуAЁЂЕуBЕФОрРыЯрЕШЃЎ
ЗжжгЪБЕуPЕНЕуAЁЂЕуBЕФОрРыЯрЕШЃЎ

 аЁбЇНЬВФШЋВтЯЕСаД№АИ
аЁбЇНЬВФШЋВтЯЕСаД№АИ аЁбЇЪ§бЇПкЫуЬтПЈЭбПкЖјГіЯЕСаД№АИ
аЁбЇЪ§бЇПкЫуЬтПЈЭбПкЖјГіЯЕСаД№АИ гХауЩњгІгУЬтПЈПкЫуЬьЬьСЗЯЕСаД№АИ
гХауЩњгІгУЬтПЈПкЫуЬьЬьСЗЯЕСаД№АИ еуНжЎаЧПЮЪБгХЛЏзївЕЯЕСаД№АИ
еуНжЎаЧПЮЪБгХЛЏзївЕЯЕСаД№АИЁОЬтФПЁПФГЩЬЕъМзЁЂввСНжжЩЬЦЗШ§ЬьЯњЪлЧщПіЕФеЫФПМЧТМШчЯТБэЃК
ШеЦк | ТєГіМзЩЬЦЗЕФЪ§СП(Иі) | ТєГіввЩЬЦЗЕФЪ§СП(Иі) | ЪеШы(дЊ) |
ЕквЛЬь | 39 | 21 | 321 |
ЕкЖўЬь | 26 | 14 | 204 |
ЕкШ§Ьь | 39 | 25 | 345 |
(1)ВЦЮёжїЙмдкКЫВщЪБЗЂЯжЃКЕквЛЬьЕФеЫФПе§ШЗЃЌЕЋЦфЫћСНЬьЕФеЫФПгавЛЬьгаЮѓЃЌЧыФуХаЖЯЕкМИЬьЕФеЫФПгаЮѓЃЌВЂЫЕУїРэгЩЃЛ
(2)ЧѓМзЁЂввСНжжЩЬЦЗЕФЕЅМлЃЎ