题目内容
如图,矩形OABC中,A(6,0)、C(0,2 )、D(0,3
)、D(0,3 ),射线l过点D且与x轴平行,点P、Q分别是l和x轴的正半轴上的动点,满足∠PQO=60º.
),射线l过点D且与x轴平行,点P、Q分别是l和x轴的正半轴上的动点,满足∠PQO=60º.
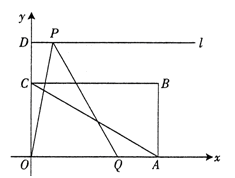
(1)点B的坐标是 ,∠CAO= º,当点Q与点A重合时,点P的坐标
为 ;
(2)设点P的横坐标为x,△OPQ与矩形OABC重叠部分的面积为S,试求S与x的函数关系式和相应的自变量x的取值范围.
 )、D(0,3
)、D(0,3 ),射线l过点D且与x轴平行,点P、Q分别是l和x轴的正半轴上的动点,满足∠PQO=60º.
),射线l过点D且与x轴平行,点P、Q分别是l和x轴的正半轴上的动点,满足∠PQO=60º.
(1)点B的坐标是 ,∠CAO= º,当点Q与点A重合时,点P的坐标
为 ;
(2)设点P的横坐标为x,△OPQ与矩形OABC重叠部分的面积为S,试求S与x的函数关系式和相应的自变量x的取值范围.
(1)(6,2 )。 30。(3,3
)。 30。(3,3 )(2)
)(2)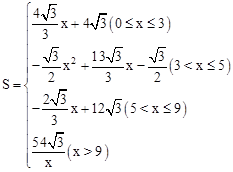
 )。 30。(3,3
)。 30。(3,3 )(2)
)(2)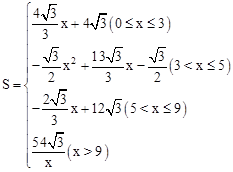
解:(1)(6,2 )。 30。(3,3
)。 30。(3,3 )。
)。
(2)当0≤x≤3时,
如图1,
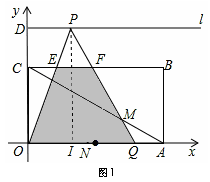
OI=x,IQ=PI•tan60°=3,OQ=OI+IQ=3+x;
由题意可知直线l∥BC∥OA,
可得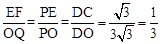 ,∴EF=
,∴EF=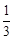 (3+x),
(3+x),
此时重叠部分是梯形,其面积为:
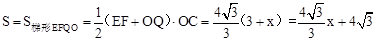
当3<x≤5时,如图2,
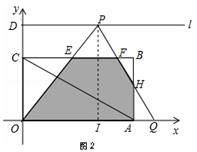
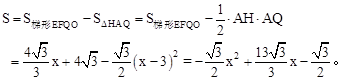
当5<x≤9时,如图3,
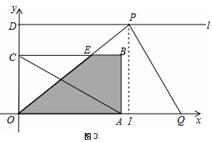
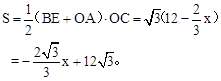
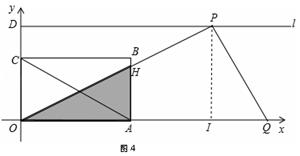
当x>9时,如图4,
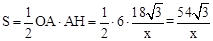 。
。
综上所述,S与x的函数关系式为:
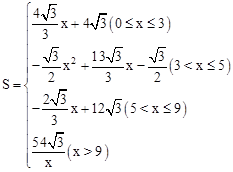 。
。
(1)①由四边形OABC是矩形,根据矩形的性质,即可求得点B的坐标:
∵四边形OABC是矩形,∴AB=OC,OA=BC,
∵A(6,0)、C(0,2 ),∴点B的坐标为:(6,2
),∴点B的坐标为:(6,2 )。
)。
②由正切函数,即可求得∠CAO的度数:
∵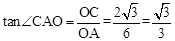 ,∴∠CAO=30°。
,∴∠CAO=30°。
③由三角函数的性质,即可求得点P的坐标;如图:当点Q与点A重合时,过点P作PE⊥OA于E,
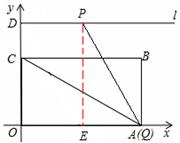
∵∠PQO=60°,D(0,3 ),∴PE=3
),∴PE=3 。
。
∴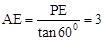 。
。
∴OE=OA﹣AE=6﹣3=3,∴点P的坐标为(3,3 )。
)。
(2)分别从当0≤x≤3时,当3<x≤5时,当5<x≤9时,当x>9时去分析求解即可求得答案。
 )。 30。(3,3
)。 30。(3,3 )。
)。(2)当0≤x≤3时,
如图1,

OI=x,IQ=PI•tan60°=3,OQ=OI+IQ=3+x;
由题意可知直线l∥BC∥OA,
可得
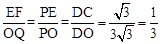 ,∴EF=
,∴EF=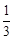 (3+x),
(3+x),此时重叠部分是梯形,其面积为:
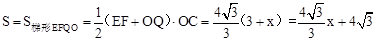
当3<x≤5时,如图2,

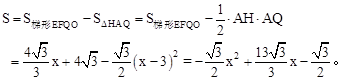
当5<x≤9时,如图3,

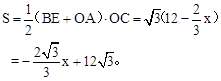
当x>9时,如图4,

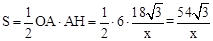 。
。综上所述,S与x的函数关系式为:
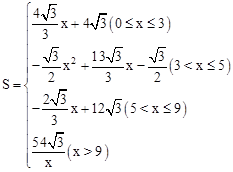 。
。(1)①由四边形OABC是矩形,根据矩形的性质,即可求得点B的坐标:
∵四边形OABC是矩形,∴AB=OC,OA=BC,
∵A(6,0)、C(0,2
 ),∴点B的坐标为:(6,2
),∴点B的坐标为:(6,2 )。
)。②由正切函数,即可求得∠CAO的度数:
∵
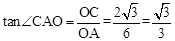 ,∴∠CAO=30°。
,∴∠CAO=30°。③由三角函数的性质,即可求得点P的坐标;如图:当点Q与点A重合时,过点P作PE⊥OA于E,

∵∠PQO=60°,D(0,3
 ),∴PE=3
),∴PE=3 。
。∴
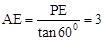 。
。∴OE=OA﹣AE=6﹣3=3,∴点P的坐标为(3,3
 )。
)。(2)分别从当0≤x≤3时,当3<x≤5时,当5<x≤9时,当x>9时去分析求解即可求得答案。

练习册系列答案
相关题目
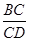 ;
;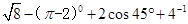 ;
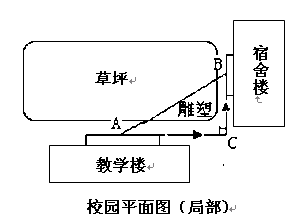
;
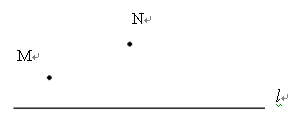
 ∠A,则AB= AC.
∠A,则AB= AC.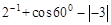 .
. ,tan220≈
,tan220≈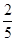 ,sin39o≈
,sin39o≈ ,tan39o≈
,tan39o≈ )
) 
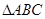 中,
中, 是
是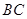 边上的高,
边上的高,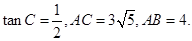 求
求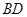 的长.(结果保留根号)
的长.(结果保留根号)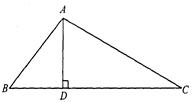
 ≈1.414,
≈1.414,  ≈1.732)
≈1.732)