��Ŀ����
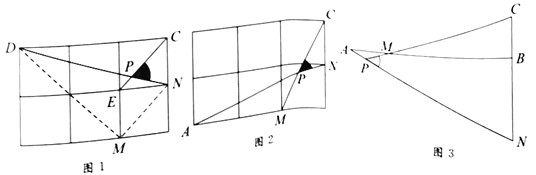
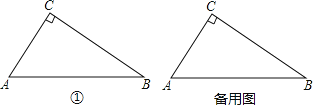
����Ŀ����ͼ�����ڡ�ABC�У���C��90�㣬AC��15��BC��20��������C����O���ABC��ÿ���߶��ཻ����O��AC�ߵ���һ��������ΪD����BC�ߵ���һ��������ΪE����AB�ߵ�����������ֱ�ΪF��G������O�İ뾶Ϊr��
��������֪��
��1���������⣬����Բ����ͼ��������һ��������������O�������������ĸ��
������̽����
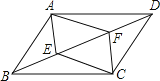
��2����֤��CD2+CE2��4r2��
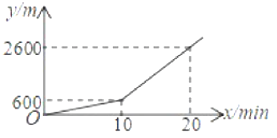
��3����r��8ʱ����CD2+CE2+FG2�����ֵΪ�� ����
���������
��4��ֱ��д�����������r��ȡֵ��Χ�����ڷ�Χ��ÿһ��ȷ����r��ֵ��CD2+CE2+FG2�������ֵ��ÿһ�����ֵ��Ӧ��Բ��O���γɵ�·����Ϊ�� ����
���𰸡���1�������������2�������������3��48����4��![]() ��
��
��������
��1������Ҫ��ͼ�μ��ɣ���ͼ����ʾ����
��2����ͼ���У�����![]() �����ù��ɶ������ɽ�����⣻
�����ù��ɶ������ɽ�����⣻
��3����Ϊ![]() �Ƕ�ֵ��
�Ƕ�ֵ��![]() ��
��![]() ���ң�
���ң�![]() �İ뾶Ϊ��ֵ 8���������ľ�ԽС����
�İ뾶Ϊ��ֵ 8���������ľ�ԽС����![]() Խ����Բ��
Խ����Բ��![]() ����
����![]() ΪԲ��8Ϊ�뾶��Բ�ϣ���
ΪԲ��8Ϊ�뾶��Բ�ϣ���![]() ʱ��
ʱ��![]() ��
��![]() ������̣���ʱ
������̣���ʱ![]() ����ɴ˼��ɽ�����⣻
����ɴ˼��ɽ�����⣻
��4������ȷ��![]() �ķ�Χ��Բ�ľ���
�ķ�Χ��Բ�ľ���![]() ���ʱ
���ʱ![]() ��ֵ����뾶�Ƚ�Сʱ��
��ֵ����뾶�Ƚ�Сʱ��![]() ��
��![]() ��ʱ
��ʱ![]() ��ֵ���Բ����
��ֵ���Բ����![]() �ϣ�Բ���þ�����
�ϣ�Բ���þ�����![]() ʱ����
ʱ����![]() ����
����![]() ��
��![]() ������
������![]() �����
�����![]() ����
����![]() ʱ����
ʱ����![]() ����
����![]() �ϣ���
�ϣ���![]() ����Բ�ڣ�Բ����
����Բ�ڣ�Բ����![]() ���ཻ���Ƴ���ʱԲ��Ӧ������
���ཻ���Ƴ���ʱԲ��Ӧ������![]() �д����ϣ��Ƴ�
�д����ϣ��Ƴ�![]() ʱ��
ʱ��![]() ��
��![]() �ϣ�
�ϣ�![]() ʱ��
ʱ��![]() ��
��![]() �д����ϣ���
�д����ϣ���![]() ��ֵ����Ƴ�
��ֵ����Ƴ�![]() ·������ͼ����
·������ͼ����![]() ��
��
��1���⣺��ͼ����Ϊ����
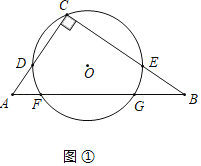
��2��֤������ͼ���У�����DE��
�ߡ�DCE��90�㣬
��DEΪ��Oֱ������DE��2r��
��CD2+CE2��DE2��4r2��

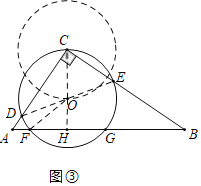
��3���⣺��ͼ���У�
��CD2+CE2�Ƕ�ֵ��FG����O���ң���O�İ뾶Ϊ��ֵ 8��
�����ľ�ԽС����FGԽ����Բ��O����CΪԲ��8Ϊ�뾶��Բ�ϣ�
��CO��ABʱ��O��AB������̣���ʱFG���
��![]() ��
��
��CH��![]() ��12��
��12��
��OC��8��
��OH��4��
OH��FG��
��![]() ��
��
��![]() ��
��
��CD2+CE2+FG2�����ֵ��![]() ��
��
�ʴ�Ϊ��448��
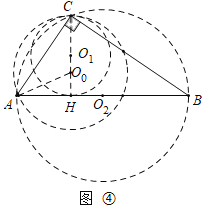
��4����ͼ���У�
����O1 ��AB����ʱ����O1��ֱ����С����СֵΪ12����ʱr��6��
��Բ��O2��AB��ʱ��Բֱ��������AB��25��
��![]() ��
��
��Բ�ľ���AB���ʱCD2+CE2+FG2��ֵ���
���뾶�Ƚ�Сʱ��O��CH��ʱCD2+CE2+FG2��ֵ���
��Բ����CH �ϣ�Բ���þ�����Aʱ����O0A��O0C��r��
��Rt��AO0H������r2����12��r��2+92��
��ã�![]() ��
��
��![]() ��
��
��![]() ʱ����O����CH�ϣ���A����Բ�ڣ�Բ����AB���ཻ��
ʱ����O����CH�ϣ���A����Բ�ڣ�Բ����AB���ཻ��
���ʱԲ��Ӧ������AC�д����ϣ�
��![]() ʱ��O��CH�ϣ�
ʱ��O��CH�ϣ�
![]() ʱ��O��AC�д����ϣ���CD2+CE2+FG2��ֵ���
ʱ��O��AC�д����ϣ���CD2+CE2+FG2��ֵ���
��O·������ͼ���� O1��O0��O2
��O1H��6��![]() ��
��
��![]() ��
��
��![]() ��AH��9��
��AH��9��
��![]() ��
��
��![]() ��
��
��O��·������![]() ��
��
�ʴ�Ϊ��![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�