题目内容
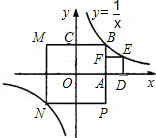
如图所示,正方形OABC,ADEF的顶点A,D,C在坐标轴上;点F在AB上,点B,E在反比例函数y=
(x>0)的图象上.
(1)正方形MNPB中心为原点O,且NP∥BM,求正方形MNPB面积.
(2)求点E的坐标.
| 1 |
| x |
(1)正方形MNPB中心为原点O,且NP∥BM,求正方形MNPB面积.
(2)求点E的坐标.

(1)因为B点在反比例函数y=
(x>0)的图象上,所以设B点坐标为(a,
),
因OABC是正方形
∴a=
,即a=±1,
∵x>0
∴a=1,B(1,1),且OA=1,
又∵正方形MNPB中心为原点O,且NP∥BM,
所以正方形MNPB面积=4×正方形OABC的面积=4×1×1=4;
(2)因ADEF是正方形,设其边长为b,
则AD=DE=b,则AD=b,
则OD=1+b,E(1+b,b)
又∵点E(1+b,b)在反比例函数y=
(x>0)的图象上,
∴b(1+b)=1即b2+b-1=0,
∴b1=
,b2=
(舍去).
即E的横坐标为1+
=
.
∴E(
,
).
| 1 |
| x |
| 1 |
| a |
因OABC是正方形
∴a=
| 1 |
| a |
∵x>0
∴a=1,B(1,1),且OA=1,
又∵正方形MNPB中心为原点O,且NP∥BM,
所以正方形MNPB面积=4×正方形OABC的面积=4×1×1=4;
(2)因ADEF是正方形,设其边长为b,
则AD=DE=b,则AD=b,
则OD=1+b,E(1+b,b)
又∵点E(1+b,b)在反比例函数y=
| 1 |
| x |
∴b(1+b)=1即b2+b-1=0,
∴b1=
| ||
| 2 |
-
| ||
| 2 |
即E的横坐标为1+
| ||
| 2 |
1+
| ||
| 2 |
∴E(
1+
| ||
| 2 |
| ||
| 2 |

练习册系列答案
相关题目