Question

【题目】如图，在正方形ABCD中，点E（与点B、C不重合）是BC边上一点，将线段EA绕点E顺时针旋转90°到EF，过点F作BC的垂线交BC的延长线于点G，连接CF．

（1）求证：△ABE≌△EGF；
（2）若AB=2，S△ABE=2S△ECF ， 求BE．

Answer 1

【答案】
（1）证明：∵EP⊥AE，

∴∠AEB+∠GEF=90°，

又∵∠AEB+∠BAE=90°，

∴∠GEF=∠BAE，

又∵FG⊥BC，

∴∠ABE=∠EGF=90°，

在△ABE与△EGF中，

，

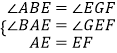∴△ABE≌△EGF（AAS）

（2）解：∵△ABE≌△EGF，AB=2，

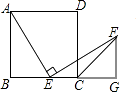
∴AB=EG=2，S△ABE=S△EGF，

∵S△ABE=2S△ECF，

∴SEGF=2S△ECF，

∴EC=CG=1，

∵四边形ABCD是正方形，

∵BC=AB=2，

∴BE=2﹣1=1．

【解析】（1）根据同角的余角相等得到一对角相等，再由一对直角相等，且AE=EF，利用AAS得到三角形ABE与三角形EFG全等；（2）利用全等三角形的性质得出AB=EG=2，S△ABE=S△EGF ， 求出SEGF=2S△ECF ， 根据三角形面积得出EC=CG=1，根据正方形的性质得出BC=AB=2，即可求出答案．此题属于四边形综合题，涉及的知识有：全等三角形的判定与性质，正方形的性质，三角形的面积，熟练掌握判定与性质是解本题的关键．