题目内容
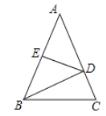
【题目】如图.在△ABC中，∠B=∠C=50°，D是BC的中点，DE⊥AB， DF⊥AC，则∠BAD=_________.
【答案】40°
【解析】
据AAS易证得△BDE≌△CDF，可得ED=FD，据三角形全等的判定HL易证得△AED≌△AFD，即可得∠EAD=∠FAD，即AD为∠BAC的角平分线，即可得∠BAD的度数．
∵D是BC的中点，
∴BD=CD，
∵DE⊥AB，DF⊥AC，
∴∠BED=∠CFD=90°，
又∵∠B=∠C=50°
∴△BDE≌△CDF(AAS)，
∴ED=FD；
又∵∠AED=∠AFD=90°，AD为公共边，
∴△AED≌△AFD（HL），
∴∠EAD=∠FAD，即AD为∠BAC的角平分线，
∴∠BAD=
(180°∠B∠C)= ×(180°50°50°)=40°.
故答案填：40°.
练习册系列答案
相关题目
