题目内容
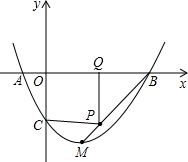
抛物线y=ax2+bx+c与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当x=0和x=2时,y的值相等.直线y=3x-7与这条抛物线相交于两点,其中一点的横坐标是4,另一点是这条抛物线的顶点M.
(1)求这条抛物线的解析式;
(2)P为线段BM上一点,过点P向x轴引垂线,垂足为Q.若点P在线段BM上运动(点P不与点B、M重合),设OQ的长为t,四边形PQOC的面积为S.求S与t之间的函数关系式及自变量t的取值范围.
(3)对于二次三项式x2-10x+36,小明同学作出如下结论:无论x取什么实数,它的值都不可能等于11.你是否同意他的说法?说明你的理由.
解:(1)①x=0和x=2时y的值相等,
∴抛物线的对称轴为x=1,
又∵抛物线的顶点M在直线y=3x-7上,
∴M(1,-4),
设抛物线的解析式为y=a(x-1)2-4,
∵直线y=3x-7与抛物线的另一个交点为(4,5),
代入y=a(x-1)2-4,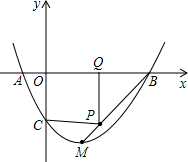
解得a=1,
∴抛物线的解析式为y=(x-1)2-4
即为:y=x2-2x-3.
(2)由y=x2-2x-3可得出,
C(0,-3),B(3,0),M(1,-4),
设直线BM的解析式为y=kx+b,把B、M两点代入求得,
直线BM的解析式为y=2x-6,
∴P(t,2t-6),QP=6-2t,CO=3,QO=t,
∴S梯形PQOC= (6-2t+3)t=-t2+
(6-2t+3)t=-t2+ t,
t,
因此S=-t2+ t,(1<t<3).
t,(1<t<3).
(3)不同意他的观点.
假设x2-10x+36=11,
解得x1=x2=5,
∴当X=5时x2-10x+36等于11,
因此无论x取什么实数,x2-10x+36的值都不可能等于11的说法是错误的.
分析①利用二次函数的对称性求出对称轴,再求出M点的坐标,设出顶点式,代入另一点可求出;
②利用抛物线的解析式,求出C、B、M点的坐标,进一步求直线BM的解析式,用t表示出P点,最后用梯形的面积计算公式解答.
假设二次三项式x2-10x+36=11,如果求出方程有解,就说明小明的说法不正确.
点评:此题利用二次函数的对称性、待定系数法、面积计算公式等知识来解决,渗透数形结合的思想.
∴抛物线的对称轴为x=1,
又∵抛物线的顶点M在直线y=3x-7上,
∴M(1,-4),
设抛物线的解析式为y=a(x-1)2-4,
∵直线y=3x-7与抛物线的另一个交点为(4,5),
代入y=a(x-1)2-4,

解得a=1,
∴抛物线的解析式为y=(x-1)2-4
即为:y=x2-2x-3.
(2)由y=x2-2x-3可得出,
C(0,-3),B(3,0),M(1,-4),
设直线BM的解析式为y=kx+b,把B、M两点代入求得,
直线BM的解析式为y=2x-6,
∴P(t,2t-6),QP=6-2t,CO=3,QO=t,
∴S梯形PQOC=
 (6-2t+3)t=-t2+
(6-2t+3)t=-t2+ t,
t,因此S=-t2+
 t,(1<t<3).
t,(1<t<3).(3)不同意他的观点.
假设x2-10x+36=11,
解得x1=x2=5,
∴当X=5时x2-10x+36等于11,
因此无论x取什么实数,x2-10x+36的值都不可能等于11的说法是错误的.
分析①利用二次函数的对称性求出对称轴,再求出M点的坐标,设出顶点式,代入另一点可求出;
②利用抛物线的解析式,求出C、B、M点的坐标,进一步求直线BM的解析式,用t表示出P点,最后用梯形的面积计算公式解答.
假设二次三项式x2-10x+36=11,如果求出方程有解,就说明小明的说法不正确.
点评:此题利用二次函数的对称性、待定系数法、面积计算公式等知识来解决,渗透数形结合的思想.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
已知点(2,8)在抛物线y=ax2上,则a的值为( )
| A、±2 | ||
B、±2
| ||
| C、2 | ||
| D、-2 |
若(2,0)、(4,0)是抛物线y=ax2+bx+c上的两个点,则它的对称轴是直线( )
| A、x=0 | B、x=1 | C、x=2 | D、x=3 |


 (2012•陕西)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(2012•陕西)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.