Question

【题目】已知：是的角平分线，点，分别在，上，且，

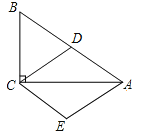
（1）如图1，求证：四边形是平行四边形；

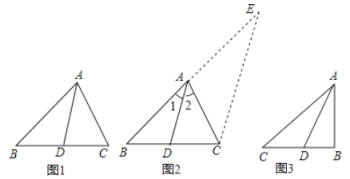
（2）如图2，若为等边三角形，在不添加辅助线的情况下，请你直接写出所有的全等三角形.

Answer 1

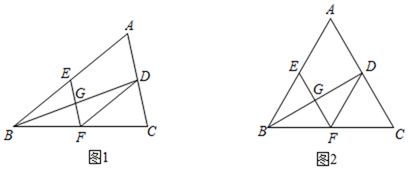
【答案】（1）详见解析；（2）△ABD≌△CBD，△BEF≌△FDC，△BGF≌△BGE，△BGE≌△DGF，△BGF≌△DGF

【解析】

（1）根据角平分线的性质及平行线的性质得到DF=BF，利用，即可求得结论；

（2）根据角平分线的性质即可证得△ABD≌△CBD；利用（1）的平行四边形的性质证得△BEF≌△FDC，再利用角平分线的性质及平行线的性质证得△BGF≌△BGE，△BGE≌△DGF，得到△BGF≌△DGF.

（1）证明：∵BD平分∠ABC，

∴∠ABD=∠DBC，

∵DF∥AB，

∴∠ABD=∠FDB，

∴∠DBC=∠FDB，

∴DF=BF，

∵BF=AE，

∴DF=AE，

∵DF∥AE，

∴四边形AEFD为平行四边形；

（2）∵为等边三角形，

∴AB=BC=AC，

∵是的角平分线，

∴∠ABD=∠CBD，

∵BD=BD，

∴△ABD≌△CBD；

由（1）知四边形AEFD为平行四边形，

∴EF∥AC,

∴∠BEF=∠A=∠C=∠BFE=60°，

∵,

∴∠DFC=∠B=60°

∴△BEF和△CDF都是等边三角形，

∵BF=DF，

∴△BEF≌△FDC；

∵是等边的角平分线，

∴∠ABD=∠CBD=30°，

∵DF∥AB,

∴∠BDF=∠ABD=30°，

∵∠BEF=∠BFE=60°，

∴∠BGE=∠BGF=∠DGF=90°，

∵BG=BG,

∴△BGF≌△BGE，

∵GF=GF,

∴△BGE≌△DGF，

∴△BGF≌△DGF