题目内容
【题目】(10分)如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,且AE∥CD,CE∥AB.
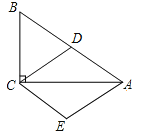
(1)四边形ADCE是菱形;
(2)若∠B=60°,BC=6,求菱形ADCE的高.(计算结果保留根号)
【答案】(1)证明见试题解析;(2)![]() .
.
【解析】
试题分析:(1)先证明四边形ADCE是平行四边形,再证明邻边相等,即可得出结论;
(2)过点D作DF⊥CE,垂足为点F;可得出△BCD是等边三角形,得出∠BDC=∠BCD=60°,CD=BC=6,再由CE∥AB,得出∠DCE=∠BDC=60°,在Rt△CDF中,由三角函数求出DF即可.
试题解析:(1)∵AE∥CD,CE∥AB,∴四边形ADCE是平行四边形,又∵∠ACB=90°,D是AB的中点,∴CD=![]() AB=BD=AD,∴平行四边形ADCE是菱形;
AB=BD=AD,∴平行四边形ADCE是菱形;
(2)过点D作DF⊥CE,垂足为点F,如图所示:DF即为菱形ADCE的高,∵∠B=60°,CD=BD,∴△BCD是等边三角形,∴∠BDC=∠BCD=60°,CD=BC=6,∵CE∥AB,∴∠DCE=∠BDC=60°,又∵CD=BC=6,∴在Rt△CDF中,DF=CDsin60°=6×![]() =
=![]() .
.

练习册系列答案
相关题目