题目内容
【题目】如图,已知点O是直线AB上的一点, ![]() ,OD、OE分别是
,OD、OE分别是![]() 、
、![]() 的角平分线.
的角平分线.
(1)求![]() 的度数;
的度数;
(2)写出图中与![]() 互余的角;
互余的角;
(3)图中有![]() 的补角吗?若有,请把它找出来,并说明理由.
的补角吗?若有,请把它找出来,并说明理由.
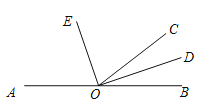
【答案】(1)70°;(2)∠DOC,∠DOB;(3)∠EOB.
【解析】试题分析:(1)利用角平分线的性质以及互补的定义得出即可;
(2)利用角平分线的性质以及互余的定义得出即可;
(3)利用角平分线的性质以及互补的定义得出即可.
试题解析:(1)∵∠BOC=40°,
∴∠AOC=140°,
∵OE是∠AOC的角平分线,
∴∠AOE的度数为:140°÷2=70°;
(2)∵OD、OE分别是∠BOC、∠AOC的角平分线,
∴∠AOE=∠EOC,∠COD=∠BOD,
∴∠EOC+∠COD=90°,
∴∠BOD+∠EOC=90°,
∴图中与∠EOC互余的角有∠DOC,∠DOB;
(3)∠COE有补角,
理由:∵∠AOE=∠EOC,∠AOE+∠BOE=180°,
∴∠COE+∠BOE=180°,
∴∠COE有补角是∠EOB.

练习册系列答案
相关题目