题目内容
【题目】如图1是一张等腰直角三角形彩色纸，将斜边上的高线四等分，然后裁出三张宽度相等的长方形纸条，若恰好可以用这些纸条为一幅正方形美术作品镶边（纸条不重叠），则这张彩色纸的面积与镶嵌所得的作品（如图2）面积之比为（ ）
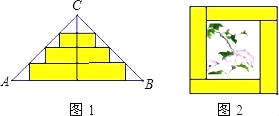
A．2：3 B．3：4 C．1：1 D．4：3
【答案】C．
【解析】
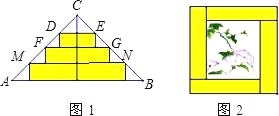
试题分析：设三张宽度相等的长方形纸条的宽为x，则等腰直角三角形的高为4x，如图1，
∴AB=8x，∴S△ABC=
4x8x=16x2，∵DE∥AB，FG∥AB，MN∥AB，
∴
=
，
=
， 
=
，∴DE=
AB=2x，FG=4x，MN=6x，
∴DE+FG+MN=2x+4x+6x=12x，∴镶嵌所得的作品的周长为12x=4x=16x，
∴镶嵌所得的作品的边长为4x，∴镶嵌所得的作品的面积=16x2，
∴这张彩色纸的面积与镶嵌所得的作品（如图2）面积之比为1：1．
故选C．
练习册系列答案
相关题目
