题目内容
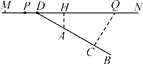
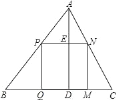
【题目】如图，△ABC是一块锐角三角形余料，边BC＝120cm，高AD＝80cm，要把它加工成一个矩形零件，使矩形PQMN的一边在BC上，其余两个顶点分别在AB、AC上．设PQ＝xcm，矩形PQMN的面积为ycm2，请写出y关于x的函数表达式（并注明x的取值范围）_____．
【答案】y＝﹣
x2+120x（0＜x＜80）
【解析】
利用DE＝PQ＝x得到AE＝80﹣x，证明△APN∽△ABC，利用相似比表示出PN＝﹣x+120，然后根据矩形的面积用x表示y即可．
解：易得四边形PQDE为矩形，则DE＝PQ＝x，
∴AE＝AD﹣AE＝80﹣x，
∵PN∥BC，
∴△APN∽△ABC，
∴
＝
，即
，
∴PN＝﹣x+120，
∴y＝x（﹣x+120）＝﹣x2+120x（0＜x＜80）．
故答案为：y＝﹣x2+120x（0＜x＜80）．
练习册系列答案
相关题目
【题目】如图，均匀的正四面体的各面依次标有1，2，3，4四个数字．小明做了60次投掷试验，结果统计如下：
朝下数字 | 1 | 2 | 3 | 4 |
出现的次数 | 16 | 20 | 14 | 10 |
（1）计算上述试验中“4朝下”的频率是 ；
（2）随机投掷正四面体两次，请用列表或画树状图法，求两次朝下的数字之和大于4的概率．
