��Ŀ����
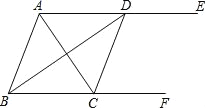
����Ŀ����ͼ1����֪������ABCD��AB=CD=4��BC=AD=6����A=��B=��C=��D=90�㣬EΪCD�ߵ��е㣬PΪ������ABCD���ϵĶ��㣬����P��A����������A��B��C��E�˶���E��ֹͣ�����P������·��Ϊx����APE�����Ϊy��
��1����x=5ʱ����Ӧy��ֵ��
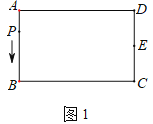
��2����ͼ2��3��4���������P�ֱ��ڱ�AB��BC��CE��ʱ��y��x֮��Ĺ�ϵʽ��

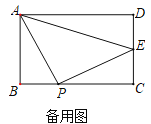
��3���籸��ͼ����P���߶�BC���˶�ʱ���Ƿ���ڵ�Pʹ�á�APE���ܳ���С�������ڣ������ʱ��PAD�Ķ������������ڣ���˵�����ɣ�
���𰸡���1��x=5ʱ��y=11��
��2������P��AB����ʱ��y=3x������P��BC����ʱ�� ![]() ������P���߶�CE��ʱ��
������P���߶�CE��ʱ�� ![]() ��
��
��3�����ڣ���ʱ��PAD=45��.
�������������������1�����������������S��AP��E=S����ABCE-S��ABP��-S��P��CE���ֱ�ó��𰸣�
��2�����õ�0��x��4ʱ����4<x��10ʱ����10<x��12ʱ���ֱ�ó�y��x�ĺ�����ϵʽ���ɣ���3��������Գ������·�ߵķ����ó�P��λ�ã������������������ε���������𰸣�
��������� (1)��ͼ1��
�߳�����ABCD�У�BC=AD=6��
�൱x=2ʱ,��AP=2,��y=S��APE=![]() ��2��6=6��
��2��6=6��
�߳�����ABCD��AB=CD=4��BC=AD=6��
�൱x=5ʱ,��BP��=1��
��y=S��AP��E=S����ABCES��ABP��S��P��CE
=![]() (AB+EC)��BC
(AB+EC)��BC![]() ��AB��BP��
��AB��BP��![]() P��C��EC=
P��C��EC=![]() (4+2)��6
(4+2)��6![]() ��1��4
��1��4![]() ��5��2=11.
��5��2=11.
(2)��0x4ʱ,y=![]() x��6=3x��
x��6=3x��
��4<x10ʱ��P��BC�ϣ�
y=S����ABCES��ABP��S��P��CE=18![]() ��4��(x4)
��4��(x4) ![]() (10x)��2=16x��
(10x)��2=16x��
��10<x��12ʱ��P��EC�ϣ�
y=![]() ��6��(12x)=363x.
��6��(12x)=363x.
����������y=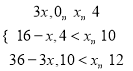 .
.
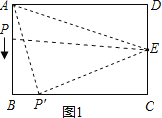
��3������.��ͼ��
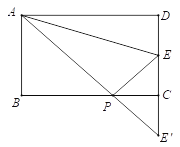
����E����BC����ֱ�ߵĶԳƵ�E��������AE�� ��BC�ڵ�P����ʱ��APE���ܳ���С������DE��=6=AD������Ϊ��D=90��������![]() =45����
=45����