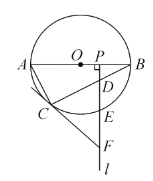
题目内容
【题目】在平面直角坐标系中,点A,B为反比例函数y=![]() (k>0,x>0)上的两个动点,以A,B为顶点构造菱形ABCD.
(k>0,x>0)上的两个动点,以A,B为顶点构造菱形ABCD.
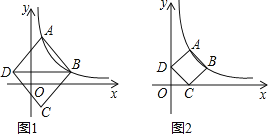
(1)如图1,点A,B横坐标分别为1,4,对角线BD∥x轴,菱形ABCD面积为![]() ,求k的值.
,求k的值.
(2)如图2,当点A,B运动至某一时刻,点C,点D恰好落在x轴和y轴正半轴上,此时∠ABC=90°,求点A,B的坐标.
【答案】(1)![]() ;(2)A(
;(2)A(![]() ,
,![]() ),点B(
),点B(![]() ,
,![]() )
)
【解析】
(1)由菱形的性质可得BD=2BE=6,AC⊥DB,由菱形的面积公式可求AC=![]() ,设点B(4,a),则点A(1,
,设点B(4,a),则点A(1,![]() +a),代入解析式可求a的值,从而求出k的值;
+a),代入解析式可求a的值,从而求出k的值;
(2)过点A作AE⊥y轴于点E,过点B作BF⊥x轴于点F,设点A(m,![]() )由全等三角形的性质可得AE=DO=CF=m,DE=OC=BF=
)由全等三角形的性质可得AE=DO=CF=m,DE=OC=BF=![]() ﹣m,可表示B坐标,代入解析式可求解.
﹣m,可表示B坐标,代入解析式可求解.
解:(1)连接AC,交BD于点E,

∵点A,B横坐标分别为1,4,对角线BD∥x轴,
∴BE=4﹣1=3,
∵四边形ABCD是菱形,
∴BD=2BE=6,AC⊥DB,
∵菱形ABCD面积为![]() ,
,
∴![]() ×BD×AC=
×BD×AC=![]() ,
,
∴AC=![]() ,
,
∴AE=CE=![]() ,
,
设点B(4,a),则点A(1,![]() +a),
+a),
∵点A,B为反比例函数y=![]() (k>0,x>0)上的两个点,
(k>0,x>0)上的两个点,
∴4a=1×(![]() +a),
+a),
∴a=![]() ,
,
∴k=4a=![]() ;
;
(2)如图,过点A作AE⊥y轴于点E,过点B作BF⊥x轴于点F,

∵四边形ABCD是菱形,∠ABC=90°,
∴四边形ABCD是正方形,
∴AD=CD=BC,∠ADC=∠DCB=90°,
∴∠ADE+∠EAD=90°,∠EDA+∠CDO=90°,∠DCO+∠CDO=90°,∠BCF+∠DCO=90°,
∴∠EAD=∠CDO=∠BCF,且∠AED=∠DOC=90°,AD=CD,
∴△AED≌△DOC(AAS),
∴AE=DO,ED=OC,
同理可得:BF=OC,CF=DO,
设点A(m,![]() ),
),
∴AE=DO=CF=m,DE=OC=BF=![]() ﹣m,
﹣m,
∴点B坐标(![]() ,
,![]() ﹣m),
﹣m),
∴![]() (
(![]() ﹣m)=
﹣m)=![]() ,
,
∴m1=![]() ,m2=﹣
,m2=﹣![]() (舍去),
(舍去),
∴点A(![]() ,
,![]() ),点B(
),点B(![]() ,
,![]() ).
).