题目内容
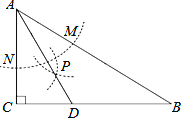
【题目】△ABC为等腰直角三角形,AB=AC,△ADE为等腰直角三角形,AD=AE,点D在直线BC上,连接CE.
(1)判断:①CE、CD、BC之间的数量关系;②CE与BC所在直线之间的位置关系,并说明理由;
(2)若D在CB延长线上,(1)中的结论是否成立?若成立,请直接写出结论,若不成立,请说明理由;
(3)若D在BC延长线上,(1)中的结论是否成立?若成立,请直接写出结论,若不成立,请写出你发现的结论,并计算:当CE=10cm,CD=2cm时,BC的长.

【答案】(1)①BC=CE+CD;②BC⊥CE,理由见解析;(2)CE⊥BC成立;BC=CD+CE不成立,结论:CD=CE+BC,理由见解析;(3)CE⊥BC成立;BC=CD+CE不成立,结论:CE=BC+CD, BC=8cm.
【解析】
(1)证明△DAB≌△EAC,即可得到BD=CE,∠B=∠ACE=45°,所以就有BC=BD+CD=CE+CD;又因∠BCE=∠ACB+∠ACE=90°,∠ABC=∠BCA=45°,得到BC⊥CF
(2)同样先证明出△DAB≌△EAC,得到BD=CE,∠ABD=∠ACE,有CD=BD+BC =CE+BC;又因∠ABD=∠ACE=180°-∠ABC=180°-45°=135°,得到∠BCE=∠ACE-∠ACB=135°-450=90°,即BC⊥CE;
(3)同样先证△DAB≌△EAC,得到BD=CE,∠ABD=∠ACE,有CE=BD=BC+CD,
又因CE=BC+CD,所以BC=CE-CD=10-2=8(cm).
(1)①BC=CE+CD;②BC⊥CE,
理由如下:∵△ABC和△ADE是等腰三角形,AB=ACAD=AE,
∵∠BAC=∠DAE=90°,∠ABC=∠BCA=45°,
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠BAD=∠CAE,
在△DAB与△EAC中,
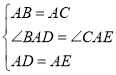 ,
,
∴△DAB≌△EAC(SAS),
∴BD=CE,∠B=∠ACE=45°,
∵BC=BD+CD,
∴BC=CE+CD,
∵∠BCE=∠ACB+∠ACE=90°,∠ABC=∠BCA=45°,
∴BC⊥CF;
(2)CE⊥BC成立;BC=CD+CE不成立,结论:CD=CE+BC,
理由如下:∵△ABC和△ADE是等腰三角形,AB=ACAD=AE,
∵∠BAC=∠DAE=90°,∠ABC=∠BCA=45°,
∴∠BAC-∠BAE=∠DAE-∠BAE,
∴∠BAD=∠CAE,
在△DAB与△EAC中,
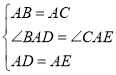 ,
,
∴△DAB≌△EAC(SAS),
∴BD=CE,∠ABD=∠ACE,
∵DC=BD+BC,
∴CD=CE+BC,
∵∠ABD=∠ACE=180°-∠ABC=180°-45°=135°,
∴∠BCE=∠ACE-∠ACB=135°-450=90°,
∴BC⊥CE;
(3)CE⊥BC成立;BC=CD+CE不成立,结论:CE=BC+CD,
同(1)可以得到△DAB≌△EAC,
∴BD=CE,∠ABD=∠ACE,
∴CE=BD=BC+CD,
∵CE=BC+CD, ∴BC=CE-CD=10-2=8(cm).

【题目】在生活与工作都离不开手机和电脑的今天,青少年近视、散光等眼问题日趋严重,为宣传2018全国爱眼日(6月6日),增强大众近视防控意识,某青少年视力矫正中心举办了主题为“永康降度还您一双明亮的眼睛”的降度明星大赛,现根据大赛公布的结果,将所有参赛孩子双眼降度之和(含近视和散光)情况绘制成了如下的统计表:
所降度数(度) | 100 | 200 | 300 | 400 | 500 | 600 |
人数(人) | 12 | 18 | 24 | 4 | 1 | 1 |
(1)求参加降度明星大赛的孩子共有多少人?
(2)求出所有参赛孩子所降度数的众数、中位数和平均数.