题目内容
在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返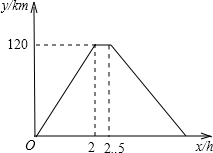 回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km).y与x的函数图象如图所示,根据图象解答下列问题:
回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km).y与x的函数图象如图所示,根据图象解答下列问题:
(1)求y与x之间的函数关系式;
(2)汽车从甲地出发,经过多长时间距离甲地100km?
(3)求这辆汽车从甲地出发4h时与乙地的距离.
 回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km).y与x的函数图象如图所示,根据图象解答下列问题:
回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km).y与x的函数图象如图所示,根据图象解答下列问题:(1)求y与x之间的函数关系式;
(2)汽车从甲地出发,经过多长时间距离甲地100km?
(3)求这辆汽车从甲地出发4h时与乙地的距离.
分析:(1)根据函数图象经过的点的坐标利用待定系数法求得函数的解析式即可,注意本题涉及到了分段函数的知识;
(2)将100代替函数关系式中的y值,求得相应的x的值即可;
(3)由图象可知,x=4时,汽车正处于返回途中,所以把x=4代入(2)中的函数解析式即可求解.
(2)将100代替函数关系式中的y值,求得相应的x的值即可;
(3)由图象可知,x=4时,汽车正处于返回途中,所以把x=4代入(2)中的函数解析式即可求解.
解答:解:(1)当0≤x≤2时,设y=k1x(k1≠0)
根据图象知函数图象经过点(2,120),
∴2k1=120,
解得k1=60,
∴y=60x,
当2<x<2.5时,y=120,
当2.5≤x≤5时,设y=k2x+b,
则
,
解得:
,
∴y=-48x+240;
(2)依题意得100=60x或100=-48x+240,(2.5≤x≤5),
解得:x=
或x=
,
答:经过
小时或
小时距离甲地100km;
(3)当x=4时y=-48×4+240=48,
120-48=72,
答:这辆汽车从甲地出发4小时与乙地距离为72km.
根据图象知函数图象经过点(2,120),
∴2k1=120,
解得k1=60,
∴y=60x,
当2<x<2.5时,y=120,
当2.5≤x≤5时,设y=k2x+b,
则
|
解得:
|
∴y=-48x+240;
(2)依题意得100=60x或100=-48x+240,(2.5≤x≤5),
解得:x=
| 5 |
| 3 |
| 35 |
| 12 |
答:经过
| 5 |
| 3 |
| 35 |
| 12 |
(3)当x=4时y=-48×4+240=48,
120-48=72,
答:这辆汽车从甲地出发4小时与乙地距离为72km.
点评:此题考查一次函数及其图象的应用,获取相关信息是解题的关键.

练习册系列答案
相关题目
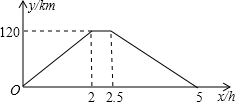 甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息,解答下列问题:
甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息,解答下列问题: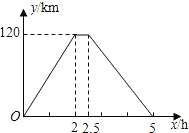 在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息,解答下列问题:
在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息,解答下列问题: 距甲地的距离为y米,y与x的函数图象如图所示.根据图象信息,解答下列问题:
距甲地的距离为y米,y与x的函数图象如图所示.根据图象信息,解答下列问题: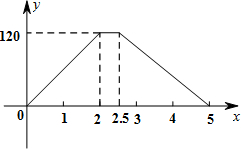 在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回,设汽车从甲地出发x(h),汽车与甲地的距离y(km),y与x的函数关系如图所示,根据信息回答下列问题:
在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回,设汽车从甲地出发x(h),汽车与甲地的距离y(km),y与x的函数关系如图所示,根据信息回答下列问题: