题目内容
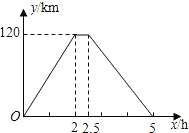 在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息,解答下列问题:
在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息,解答下列问题:(1)这辆汽车的往、返速度是否相同?请说明理由;
(2)求返程中y与x之间的函数表达式;
(3)求这辆汽车从甲地出发4h时与甲地的距离.
分析:(1)由图象可知,去时用了2小时,返回时用了5-2.5=2.5小时,而路程相等,所以往返速度不同;
(2)可设该段函数解析式为y=kx+b.因为图象过点(2.5,120),(5,0),列出方程组即可求解;
(3)由图象可知,x=4时,汽车正处于返回途中,所以把x=4代入(2)中的函数解析式即可求解.
(2)可设该段函数解析式为y=kx+b.因为图象过点(2.5,120),(5,0),列出方程组即可求解;
(3)由图象可知,x=4时,汽车正处于返回途中,所以把x=4代入(2)中的函数解析式即可求解.
解答:解:(1)不同.理由如下:
∵往、返距离相等,去时用了2小时,而返回时用了2.5小时,
∴往、返速度不同(2分)
(2)设返程中y与x之间的表达式为y=kx+b,
则
,解之,得
. (5分)
∴y=-48x+240.(2.5≤x≤5)(评卷时,自变量的取值范围不作要求)(6分)
(3)当x=4时,汽车在返程中,∴y=-48×4+240=48.
∴这辆汽车从甲地出发4h时与甲地的距离为48km.(8分)
∵往、返距离相等,去时用了2小时,而返回时用了2.5小时,
∴往、返速度不同(2分)
(2)设返程中y与x之间的表达式为y=kx+b,
则
|
|
∴y=-48x+240.(2.5≤x≤5)(评卷时,自变量的取值范围不作要求)(6分)
(3)当x=4时,汽车在返程中,∴y=-48×4+240=48.
∴这辆汽车从甲地出发4h时与甲地的距离为48km.(8分)
点评:本题需仔细分析图象,利用待定系数法解决问题.

练习册系列答案
相关题目
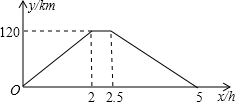 甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息,解答下列问题:
甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息,解答下列问题: 距甲地的距离为y米,y与x的函数图象如图所示.根据图象信息,解答下列问题:
距甲地的距离为y米,y与x的函数图象如图所示.根据图象信息,解答下列问题: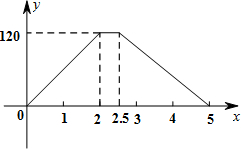 在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回,设汽车从甲地出发x(h),汽车与甲地的距离y(km),y与x的函数关系如图所示,根据信息回答下列问题:
在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回,设汽车从甲地出发x(h),汽车与甲地的距离y(km),y与x的函数关系如图所示,根据信息回答下列问题: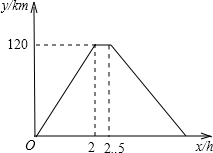 回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km).y与x的函数图象如图所示,根据图象解答下列问题:
回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km).y与x的函数图象如图所示,根据图象解答下列问题: