题目内容
【题目】完成下面推理过程：
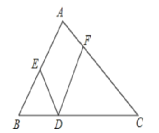
如图，已知DE∥BC，DF、BE分别平分∠ADE、∠ABC，可推得∠FDE=∠DEB的理由：
∵DE∥BC（已知）
∴∠ADE= （ ）
∵DF、BE分别平分∠ADE、∠ABC，
∴∠ADF=
（ ）
∠ABE= （ ）
∴∠ADF=∠ABE
∴ ∥ （ ）
∴∠FDE=∠DEB．（ ）
【答案】∠ABC，两直线平行，同位角相等；∠ADE，∠ABC，角平分线的定义；DF，BE，同位角相等，两直线平行；两直线平行，内错角相等
【解析】
根据平行线的性质由DE∥BC得∠ADE=∠ABC，再根据角平分线的定义得到∠ADF=
∠ADE，∠ABE=∠ABC，则∠ADF=∠ABE，然后根据平行线的判定得到
DF∥BE，最后利用平行线的性质得∠FDE=∠DEB．
∵DE∥BC，
∴∠ADE=∠ABC，
∵DF、BE分别平分∠ADE、∠ABC，
∴∠ADF=∠ADE，
∠ABE=∠ABC，
∴∠ADF=∠ABE，
∴DF∥BE，
∴∠FDE=∠DEB．
故答案为∠ABC，两直线平行，同位角相等；∠ADE，∠ABC，角平分线的定义；DF，BE，同位角相等，两直线平行；两直线平行，内错角相等．
练习册系列答案
相关题目
