题目内容
【题目】已知BF平分![]() 的外角
的外角![]() ,D为射线BF上一动点.
,D为射线BF上一动点.
(1)如图所示,若![]() ,求证:
,求证:![]() ;
;

(2)在D点运动的过程中,试比较![]() 与
与![]() 的大小,并说明你的理由.
的大小,并说明你的理由.

【答案】(1)证明见解析;(2)![]() .理由见解析.
.理由见解析.
【解析】
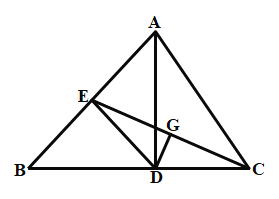
(1)在BE上取点M,使BM=BA,连接DM,可证明△ADB≌△MDB,可得DM=DC,可证得∠DAB=∠DCB,再结合三角形内角和定理可证得结论;
(2)由(1)可得到DM=DC,在△DMC中,可得DM+DC>BM+BC,则有DA+DC>BA+BC,可得出结论.
解:(1)证明:如图1,在BE上取点M,使BM=BA,连接DM,
∵BF平分∠ABE,
∴∠ABD=∠MBD,
在△ABD和△MBD中,
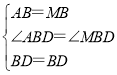
∴△ABD≌△MBD(SAS),
∴DM=DA,∠DAB=∠DMB,
又∵DA=DC,
∴DM=DC,
∴∠DMB=∠DCB,
∴∠DAB=∠DCB,
∴∠ABC=∠ADC;
(2)![]() .
.
理由如下:
在(1)中可得△ABD≌△MBD,
∴AD=MD,AB=MB,
在△DMC中,由三角形三边关系可得DM+DC>MC,
∴DM+DC>MB+BC,
∴DA+DC>BA+BC,
即BA+BC<DA+DC.

练习册系列答案
相关题目