题目内容
如图(1),在正方形ABCD中,M为AB的中点,E为AB延长线上一点,MN⊥DM,且交∠CBE的平分线于点N.
(1)DM与MN相等吗?试说明理由.
(2)若将上述条件“M为AB的中点”改为“M为AB上任意一点”,其余条件不变,如图(2),则DM与MN相等吗?为什么?
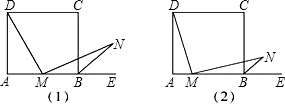
(1)DM与MN相等吗?试说明理由.
(2)若将上述条件“M为AB的中点”改为“M为AB上任意一点”,其余条件不变,如图(2),则DM与MN相等吗?为什么?
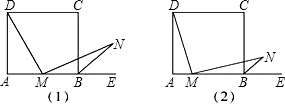
(1)过N作NF⊥AE于F,MN交BC于H,

∵HB∥NF,MN⊥DM,
∴可得∠BMH=∠MDA,
∴△MBH∽△DAM,△MBH∽△MFN
∴
=
=
=
,
∴2NF=MF,
又∵NF=BF,
∴MB=BF=
DA,
由以上可得△DAM≌△MFN
即可得DM=MN;
(2)结论“DM=MN”仍成立.
证明:
在AD上截取AF'=AM,连接F'M.
∵DF'=AD-AF',MB=AB-AM,AD=AB,AF'=AM,
∴DF'=MB ,
,
∵∠F'DM+∠DMA=∠BMN+∠DMA=90°,
∴∠F'DM=∠BMN,
∵AF′=AM,∠A=90°,
∴∠AF′M=∠AMF′=45°,
∴∠DF′M=135°,
∵BN平分∠CBE,∠CBE=90°,
∴∠NBE=
∠CBE=45°,
∴∠MBN=135°,
∴∠DF′M=∠MBN,
在△DF'M和△MBN中
,
∴△DF'M≌△MBN.
∴DM=MN.

∵HB∥NF,MN⊥DM,
∴可得∠BMH=∠MDA,
∴△MBH∽△DAM,△MBH∽△MFN
∴
| BH |
| MB |
| AM |
| DA |
| 1 |
| 2 |
| NF |
| MF |
∴2NF=MF,
又∵NF=BF,
∴MB=BF=
| 1 |
| 2 |
由以上可得△DAM≌△MFN
即可得DM=MN;
(2)结论“DM=MN”仍成立.
证明:
在AD上截取AF'=AM,连接F'M.
∵DF'=AD-AF',MB=AB-AM,AD=AB,AF'=AM,
∴DF'=MB
 ,
,∵∠F'DM+∠DMA=∠BMN+∠DMA=90°,
∴∠F'DM=∠BMN,
∵AF′=AM,∠A=90°,
∴∠AF′M=∠AMF′=45°,
∴∠DF′M=135°,
∵BN平分∠CBE,∠CBE=90°,
∴∠NBE=
| 1 |
| 2 |
∴∠MBN=135°,
∴∠DF′M=∠MBN,
在△DF'M和△MBN中
|
∴△DF'M≌△MBN.
∴DM=MN.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目










