题目内容
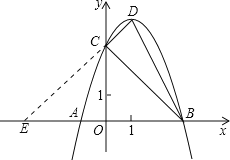
【题目】如图,二次函数![]() 的图象与x轴交于A、B两点,与y轴交于点C,顶点为D,
的图象与x轴交于A、B两点,与y轴交于点C,顶点为D,
(1)求点A,B,C的坐标.
(2)求△BCD的面积

【答案】(1)A(-1,0)B(3,0) C(0,3)
(2)△BCD的面积为3.
【解析】试题分析:(1)分别令y=0,x=0,即可求出A.B.C点的坐标.
(2)延长DC交x轴于E,利用S△BCD=S△BED-S△BCE计算即可
(1)令y=0,可得x=3或x=﹣1. 令x=0,可得y=3.
∴A(-1,0)B(3,0) C(0,3)
(2)依题意,可得y=-x2+2x+3=-(x-1)2+4.
∴顶点D(1,4).
令y=0,可得x=3或x=-1.
∴令x=0,可得y=3.
∴C(0,3).
∴OC=3,
∴直线DC的解析式为y=x+3.
设直线DE交x轴于E.
∴BE=6.
∴S△BCD=S△BED-S△BCE=3.
∴△BCD的面积为3.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
