题目内容
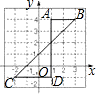 如图,已知A(1,4),B(3,4),C(-2,-1),D(1,-1),那么△ABE与△CDE的面积比是
如图,已知A(1,4),B(3,4),C(-2,-1),D(1,-1),那么△ABE与△CDE的面积比是
- A.

- B.
- C.

- D.

C
分析:由于点A与点B的纵坐标相同,可知AB⊥y轴,同理CD⊥y轴,则AB∥CD,易证△ABE∽△DCE,根据相似三角形的面积的比等于相似比的平方,得出△ABE与△CDE的面积比是(AB:CD)2.
解答: 解:∵A(1,4),B(3,4),即点A与点B的纵坐标相同,
解:∵A(1,4),B(3,4),即点A与点B的纵坐标相同,
∴AB⊥y轴,且AB=2,
同理CD⊥y轴,CD=3,
∴AB∥CD,
∴∠A=∠D,∠B=∠C,
∴△ABE∽△DCE,
∴△ABE与△CDE的面积比=(AB:CD)2=(2:3)2=4:9.
故选C.
点评:本题结合平面直角坐标系考查了相似三角形的判定及性质.
有两角对应相等的两个三角形相似.
相似三角形面积的比等于相似比的平方.
分析:由于点A与点B的纵坐标相同,可知AB⊥y轴,同理CD⊥y轴,则AB∥CD,易证△ABE∽△DCE,根据相似三角形的面积的比等于相似比的平方,得出△ABE与△CDE的面积比是(AB:CD)2.
解答:
 解:∵A(1,4),B(3,4),即点A与点B的纵坐标相同,
解:∵A(1,4),B(3,4),即点A与点B的纵坐标相同,∴AB⊥y轴,且AB=2,
同理CD⊥y轴,CD=3,
∴AB∥CD,
∴∠A=∠D,∠B=∠C,
∴△ABE∽△DCE,
∴△ABE与△CDE的面积比=(AB:CD)2=(2:3)2=4:9.
故选C.
点评:本题结合平面直角坐标系考查了相似三角形的判定及性质.
有两角对应相等的两个三角形相似.
相似三角形面积的比等于相似比的平方.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
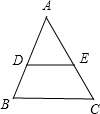 如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )
如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
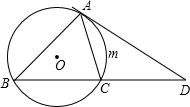 =2,∠ADC=30°
=2,∠ADC=30°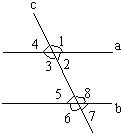 30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
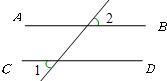 13、如图,已知直线AB∥CD,∠1=50°,则∠2=
13、如图,已知直线AB∥CD,∠1=50°,则∠2=