Question

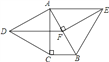
【题目】如图，分别以Rt△ABC的直角边AC及斜边AB为边向外作等边△ACD、等边△ABE，EF⊥AB，垂足为F，连接DF，当=____时，四边形ADFE是平行四边形．

Answer 1

【答案】．

【解析】试题分析：当=时，四边形ADFE是平行四边形．理由如下：

∵=，∴∠CAB=30°，∵△ABE为等边三角形，EF⊥AB，∴EF为∠BEA的平分线，∠AEB=60°，AE=AB，∴∠FEA=30°，又∠BAC=30°，∴∠FEA=∠BAC，在△ABC和△EAF中，∵∠ACB=∠EFA，∠BAC=∠AEF，AB=AE，∴△ABC≌△EAF（AAS），∵∠BAC=30°，∠DAC=60°，∴∠DAB=90°，即DA⊥AB，∵EF⊥AB，∴AD∥EF，∵△ABC≌△EAF，∴EF=AC=AD，∴四边形ADFE是平行四边形．故答案为： ．