Question

【题目】如图，是⊙的直径，点在的延长线上，是⊙上的两点，，，延长交的延长线于点．

（1）求证:是⊙的切线；

（2）求证:；

（3）若，求弦的长．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）．

【解析】

（1）连接OC，可证得∠CAD＝∠BCD，由∠CAD＋∠ABC＝90，可得出∠OCD＝90，即结论得证；

（2）证明△ABC≌△AFC可得CB＝CF，又CB＝CE，则CE＝CF；

（3）证明△DCB∽△DAC，可求出DA的长，求出AB长，设BC＝a，AC＝a，则由勾股定理可得AC的长．

（1）连接OC，

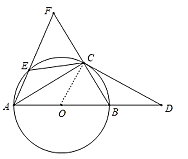
∵AB是⊙O的直径，

∴∠ACB＝90，

∴∠CAD＋∠ABC＝90，

∵CE＝CB，

∴∠CAE＝∠CAB，

∵∠BCD＝∠CAE，

∴∠CAB＝∠BCD，

∵OB＝OC，

∴∠OBC＝∠OCB，

∴∠OCB＋∠BCD＝90，

∴∠OCD＝90，

∴CD是⊙O的切线；

（2）∵∠BAC＝∠CAE，∠ACB＝∠ACF＝90，AC＝AC，

∴△ABC≌△AFC（ASA），

∴CB＝CF，

又∵CB＝CE，

∴CE＝CF；

（3）∵∠BCD＝∠CAD，∠ADC＝∠CDB，

∴△DCB∽△DAC，

∴

∴=，

∴DA＝6，

∴

∴AB＝ADBD＝63＝3，

设BC＝a，AC＝a，由勾股定理可得：a2＋(a)2＝32，

解得：a＝，

∴AC＝．