题目内容
 完成填空,如图AB∥CD,AE平分∠BAC,CE平分∠ACD.求证:AE⊥CE.
完成填空,如图AB∥CD,AE平分∠BAC,CE平分∠ACD.求证:AE⊥CE.
证明:∵AB∥CD
∴∠BAC+∠ACD=180°________
∵AE平分∠BAC,CE平分∠ACB________
∴∠1= ∠BAC,∠2=
∠BAC,∠2= ∠ACD
∠ACD
∴∠1+∠2= ∠BAC+
∠BAC+ ∠ACD
∠ACD
= (∠BAC+∠ACD)
(∠BAC+∠ACD)
= ×180°
×180°
=90°
∵∠1+∠2+∠E=180°________
∴∠E=180°-(∠1+∠2)
=180°-90°
=90°
∴AE⊥CE________.
两直线平行,同旁内角互补 已知 三角形内角和定理 垂直的定义
分析:由AB∥CD,根据两直线平行,同旁内角互补,即可得∠BAC+∠ACD=180°,又由AE平分∠BAC,CE平分∠ACD,即可求得∠1+∠2=90°,然后由三角形的内角和定理,即可求得∠E=90°,继而可证得AE⊥CE.
解答:证明:∵AB∥CD,
∴∠BAC+∠ACD=180° (两直线平行,同旁内角互补),
∵AE平分∠BAC,CE平分∠ACB( 已知),
∴∠1= ∠BAC,∠2=
∠BAC,∠2= ∠ACD,
∠ACD,
∴∠1+∠2= ∠BAC+
∠BAC+ ∠ACD
∠ACD
= (∠BAC+∠ACD)
(∠BAC+∠ACD)
= ×180°
×180°
=90°,
∵∠1+∠2+∠E=180° (三角形内角和定理)
∴∠E=180°-(∠1+∠2)
=180°-90°
=90°,
∴AE⊥CE (垂直的定义).
故答案为:两直线平行,同旁内角互补;已知;三角形内角和定理;垂直的定义.
点评:此题考查了平行线的性质、三角形内角和定理以及垂直的定义.此题难度不大,注意掌握数形结合思想的应用.
分析:由AB∥CD,根据两直线平行,同旁内角互补,即可得∠BAC+∠ACD=180°,又由AE平分∠BAC,CE平分∠ACD,即可求得∠1+∠2=90°,然后由三角形的内角和定理,即可求得∠E=90°,继而可证得AE⊥CE.
解答:证明:∵AB∥CD,
∴∠BAC+∠ACD=180° (两直线平行,同旁内角互补),
∵AE平分∠BAC,CE平分∠ACB( 已知),
∴∠1=
 ∠BAC,∠2=
∠BAC,∠2= ∠ACD,
∠ACD,∴∠1+∠2=
 ∠BAC+
∠BAC+ ∠ACD
∠ACD=
 (∠BAC+∠ACD)
(∠BAC+∠ACD)=
 ×180°
×180°=90°,
∵∠1+∠2+∠E=180° (三角形内角和定理)
∴∠E=180°-(∠1+∠2)
=180°-90°
=90°,
∴AE⊥CE (垂直的定义).
故答案为:两直线平行,同旁内角互补;已知;三角形内角和定理;垂直的定义.
点评:此题考查了平行线的性质、三角形内角和定理以及垂直的定义.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 =
= (2013•桥西区模拟)注意:为了使同学们更好地解答本题,下面提供了一种解题思路,你可以依照这个思路填空,并完成本题解答的全过程.如果你选用其他的解题方案,此时,不必填空,只需按照解答题的一般要求,进行解答即可.
(2013•桥西区模拟)注意:为了使同学们更好地解答本题,下面提供了一种解题思路,你可以依照这个思路填空,并完成本题解答的全过程.如果你选用其他的解题方案,此时,不必填空,只需按照解答题的一般要求,进行解答即可.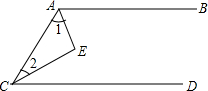 完成填空,如图AB∥CD,AE平分∠BAC,CE平分∠ACD.求证:AE⊥CE.
完成填空,如图AB∥CD,AE平分∠BAC,CE平分∠ACD.求证:AE⊥CE.