题目内容
【题目】如图，抛物线y=﹣ 
x2+bx+c与一次函数y=﹣x+4分别交y轴、x轴于A、B两点．
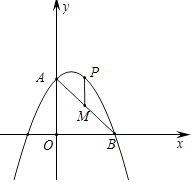
（1）求这个抛物线的解析式；
（2）设P（x，y）是抛物线在第一象限内的一个动点，过点P作直线PH⊥x轴于点H，交直线AB于点M．
①求当x取何值时，PM有最大值？最大值是多少？
②当PM取最大值时，以A、P、M、N为顶点构造平行四边形，求第四个顶点N的坐标．
【答案】
（1）
解：∵一次函数y=﹣x+4分别交y轴、x轴于A、B两点，
∴A（0，4），B（4，0），
把A（0，4），B（4，0）代入y=﹣ 
x2+bx+c可得 
，
解得 
，
∴抛物线的解析式为y=﹣ x2+x+4
（2）
解：①如图1中，设P（x，﹣ x2+x+4），则M（x，﹣x+4）．
∴PM=﹣ x2+m+4﹣（﹣x+4）=﹣ x2+2x=﹣ （x﹣2）2+2，
∵﹣ ＜0，
∴x=2时，pM的值最大，最大值为2．
②由①可知P（2，4），M（2，2），
当以A、P、M、N为顶点的四边形为平行四边形时，N1（0，6），N2（4，2），N3（0，2）．
【解析】（1）由直线解析式可求得A、B的坐标，再利用待定系数法可求得抛物线的解析式；（2）①可利用x表示出点M的坐标，构建二次函数即可解决问题．②画出图形，满足条件的点N有三个．
【考点精析】掌握二次函数的性质是解答本题的根本，需要知道增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．
练习册系列答案
相关题目
