题目内容
 (2013•葫芦岛)如图,AB是半圆的直径,AB=2,∠B=30°,则
(2013•葫芦岛)如图,AB是半圆的直径,AB=2,∠B=30°,则 |
| BC |
分析:首先连接CO,再利用圆周角定理计算出圆心角∠COB的度数,然后利用弧长公式进行计算即可.
解答: 解:连接CO,
解:连接CO,
∵AB=2,
∴OB=1,
∵AB是半圆的直径,
∴∠ACB=90°,
∵∠B=30°,
∴∠A=60°,
∴∠COB=120°,
∴
=
=
π,
故选:B.
 解:连接CO,
解:连接CO,∵AB=2,
∴OB=1,
∵AB是半圆的直径,
∴∠ACB=90°,
∵∠B=30°,
∴∠A=60°,
∴∠COB=120°,
∴
 |
| BC |
| 120•π•1 |
| 180 |
| 2 |
| 3 |
故选:B.
点评:此题主要考查了圆周角定理,以及弧长计算,关键是掌握圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.

练习册系列答案
相关题目
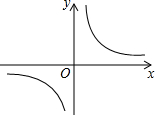 (2013•葫芦岛)如图是反比例函数y=
(2013•葫芦岛)如图是反比例函数y=