题目内容
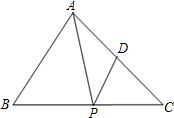 (1996•山东)如图,在△ABC中,BC=6,AC=4
(1996•山东)如图,在△ABC中,BC=6,AC=4| 2 |
(1)求y与x之间的函数关系式,并指出自变量x的取值范围.
(2)是否存在这样的P点,使得△APD的面积等于△ABP面积的
| 2 |
| 3 |
分析:(1)设△ABP,△APD,△CDP的面积分别记为S1,S2,S3,由已知条件可求出△ABC中BC边上的高为4,设△CDP中PC边上的高为h,找到h和x的数量关系,则即可求出用x的代数式分别表示S1,S2,S3进而表示出△APD的面积y;
(2)存在,有(1)可知AE=4,进而求出S△ABP=
BP•AN=
•4=2x,当使得△APD的面积等于△ABP面积的
时,则-
x2+2x=
•2x,再解一元二次方程即可求出BP的长.
(2)存在,有(1)可知AE=4,进而求出S△ABP=
| 1 |
| 2 |
| x |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
解答:解:(1)过A作AE⊥BC,则AE为BC边上的高,
由Rt△AEC中,AC=4
,得到此三角形为等腰直角三角形,
∴sin45°=
,即AE=ACsin45°=4
×
=4,
∴△ABC中BC边上的高为4,
设△CDP中PC边上的高为h,
∵PD∥AB,
∴△CDP∽△CAB,
∴
=
,
∴h=
(6-x)
这样S1=2x,S3=
(6-x)•
6-x)=
(6-x)2,
S2=12-2x-
(6-x)2,
即y=-
x2+2x,
∵P点只能在线段BC上移动,且不能与B、C两点重合
∴函数自变量的取值范围是0<x<6;
(2)由(1)可知AE=4,
∴S△ABP=
BP•AE=
•4=2x,
若S△APD=
S△ABP则-
x2+2x=
•2x
即x2-2x=0解得x1=2,x2=0(舍去)
∵0<2<6,
∴在BC边上存在一点P(BP=2),使△APD的面积等于△ABP的面积的
.

由Rt△AEC中,AC=4
| 2 |
∴sin45°=
| AE |
| AC |
| 2 |
| ||
| 2 |
∴△ABC中BC边上的高为4,
设△CDP中PC边上的高为h,
∵PD∥AB,
∴△CDP∽△CAB,
∴
| h |
| 4 |
| 6-x |
| 6 |
∴h=
| 2 |
| 3 |
这样S1=2x,S3=
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
S2=12-2x-
| 1 |
| 3 |
即y=-
| 1 |
| 3 |
∵P点只能在线段BC上移动,且不能与B、C两点重合
∴函数自变量的取值范围是0<x<6;
(2)由(1)可知AE=4,
∴S△ABP=
| 1 |
| 2 |
| x |
| 2 |
若S△APD=
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
即x2-2x=0解得x1=2,x2=0(舍去)
∵0<2<6,
∴在BC边上存在一点P(BP=2),使△APD的面积等于△ABP的面积的
| 2 |
| 3 |
点评:本题考查了二次函数和一元二次方程的关系以及三角形的面积,难度不大,属于中档题目.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
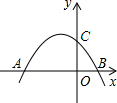 (1996•山东)如图抛物线y=ax2+bx+c,若OB=OC=
(1996•山东)如图抛物线y=ax2+bx+c,若OB=OC= (1996•山东)已知如图,相互线段a和b.求作:△ABC,使AB=AC=a,BC边上的中线等于b.(写出作法,保留作图痕迹,不要求证明)
(1996•山东)已知如图,相互线段a和b.求作:△ABC,使AB=AC=a,BC边上的中线等于b.(写出作法,保留作图痕迹,不要求证明)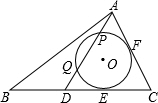 (1996•山东)如图,在△ABC中,BC>AC,⊙O分别切BC、AC于E、F,D是线段BE上的一点,AD交⊙O于P、Q两点,即AP=DQ,求证:∠B=∠DAC-∠DAB.
(1996•山东)如图,在△ABC中,BC>AC,⊙O分别切BC、AC于E、F,D是线段BE上的一点,AD交⊙O于P、Q两点,即AP=DQ,求证:∠B=∠DAC-∠DAB.