题目内容
如图已知抛物线y=mx2+nx+p与y=x2+6x+5关于y轴对称,并与y轴交于 点M,与x轴交于点A和B.
点M,与x轴交于点A和B.
(1)求出y=mx2+nx+p的解析式,试猜想出一般形式y=ax2+bx+c关于y轴对称的二次函数解析式(不要求证明);
(2)若AB中点是C,求sin∠CMB;
(3)如果一次函数y=kx+b过点M,且于y=mx2+nx+p相交于另一点N(i,j),如果i≠j,且i2-i+z=0和j2-j+z=0,求k的值.
解:(1)抛物线的解析式是y=x2-6x+5,y=ax2+bx+c关于y轴对称的二次函数解析式为:y=ax2-bx+c.
(2)当y=0时x2-6x+5=0x1=1x2=5所以A(1,0)B(5,0)C是AB的中点所以C(3,0)又因为OB=OM=5?△OMB是等腰△过0作OE⊥MB?OE∥CD因为∠EOB=45度,所以∠DCB=45度?CD= Rt△OMC中OM=5,OC=3所以MC=
Rt△OMC中OM=5,OC=3所以MC= =
= ,
,
∴sin .
.
(3) ,即
,即 ,
,
又因为N在y=kx+b上
又∵j=ki+bM在y=kx+b上,
∴b=5,
∴j=ki+5?1-i=ki+5?k=-1- ,
,
又∵N在y=x2-6x+5上,
所以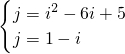 ,
,
即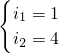 ,即
,即 .
.
分析:(1)抛物线y=mx2+nx+p与y=x2+6x+5关于y轴对称,知关于y轴对称x变为-x,y轴值不变,所以易得y=x2+6(-x)+5,即对称后的表达式为y=ax2+bx+c,关于y轴对称只要把x变为-x就可以了;
(2)作辅助线过0作OE⊥MB,把∠CMB转化到直角三角形中计算,就行了;
(3)根据已知关系解方程组得b值,最后待定系数求出k的值.
点评:此题考查函数图象对称问题和函数性质,运用转化思想把角放到直角三角形里解,点在函数上用待定系数求出各点坐标,从而求出k值,方法简单,过程较复杂.
(2)当y=0时x2-6x+5=0x1=1x2=5所以A(1,0)B(5,0)C是AB的中点所以C(3,0)又因为OB=OM=5?△OMB是等腰△过0作OE⊥MB?OE∥CD因为∠EOB=45度,所以∠DCB=45度?CD=
 Rt△OMC中OM=5,OC=3所以MC=
Rt△OMC中OM=5,OC=3所以MC= =
= ,
,∴sin
 .
.(3)
 ,即
,即 ,
,
又因为N在y=kx+b上
又∵j=ki+bM在y=kx+b上,
∴b=5,
∴j=ki+5?1-i=ki+5?k=-1-
 ,
,又∵N在y=x2-6x+5上,
所以
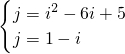 ,
,即
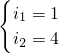 ,即
,即 .
.分析:(1)抛物线y=mx2+nx+p与y=x2+6x+5关于y轴对称,知关于y轴对称x变为-x,y轴值不变,所以易得y=x2+6(-x)+5,即对称后的表达式为y=ax2+bx+c,关于y轴对称只要把x变为-x就可以了;
(2)作辅助线过0作OE⊥MB,把∠CMB转化到直角三角形中计算,就行了;
(3)根据已知关系解方程组得b值,最后待定系数求出k的值.
点评:此题考查函数图象对称问题和函数性质,运用转化思想把角放到直角三角形里解,点在函数上用待定系数求出各点坐标,从而求出k值,方法简单,过程较复杂.

练习册系列答案
相关题目
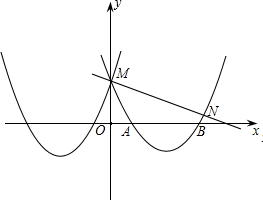 点M,与x轴交于点A和B.
点M,与x轴交于点A和B. 如图已知抛物线y=ax2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,3).设抛物线的顶点为D,求解下列问题:
如图已知抛物线y=ax2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,3).设抛物线的顶点为D,求解下列问题: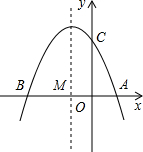 如图已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C.
如图已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C.