题目内容
 如图已知抛物线y=ax2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,3).设抛物线的顶点为D,求解下列问题:
如图已知抛物线y=ax2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,3).设抛物线的顶点为D,求解下列问题:(1)求抛物线的解析式和D点的坐标;
(2)过点D作DF∥y轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;
(3)能否在抛物线上找到一点Q,使△BDQ为直角三角形?若能找到,试写出Q点的坐标;若不能,请说明理由.
分析:(1)可根据A,B的坐标,用交点式二次函数通式来设出抛物线的解析式,进而可得出D的坐标;
(2)将B点代入,求出F点的坐标(1,2),进而得出DF的长,以及△BCD的面积;
(3)本题要分三种情况进行讨论.
①当∠BDQ=90°时,此时DQ是圆G的切线,设DQ交y轴于M,那么可通过求直线DM的解析式,然后联立抛物线的解析式即可求出Q点的坐标.
②当∠DBQ=90°时,可过Q作x轴的垂线,设垂足为P,先设出Q点的坐标,然后根据相似三角形DHB和BPQ得出的关于DH,BP,BH,PQ的比例关系式,求出Q点的坐标.
③当∠BQD=90°时,显然此时Q,C重合,因此Q点的坐标即为C点的坐标.综上所述可得出符合条件的Q点的坐标.
(2)将B点代入,求出F点的坐标(1,2),进而得出DF的长,以及△BCD的面积;
(3)本题要分三种情况进行讨论.
①当∠BDQ=90°时,此时DQ是圆G的切线,设DQ交y轴于M,那么可通过求直线DM的解析式,然后联立抛物线的解析式即可求出Q点的坐标.
②当∠DBQ=90°时,可过Q作x轴的垂线,设垂足为P,先设出Q点的坐标,然后根据相似三角形DHB和BPQ得出的关于DH,BP,BH,PQ的比例关系式,求出Q点的坐标.
③当∠BQD=90°时,显然此时Q,C重合,因此Q点的坐标即为C点的坐标.综上所述可得出符合条件的Q点的坐标.
解答: 解:(1)设抛物线的解析式为y=a(x+1)(x-3),
解:(1)设抛物线的解析式为y=a(x+1)(x-3),
把(0,3)代入,
解得a=-1,
解析式为y=-x2+2x+3,
则点D的坐标为(1,4),
(2)设直线BC的解析式为y=kx+3,把B(3,0)代入,
解得k=-1,所以F(1,2),
∴DF=4-2=2,
△BCD的面积=
×2×1+
×2×2=3;
(3)①点C即在抛物线上,CD=
,BC=3
,BD=2
.
∵CD2+BC2=20,BD2=20,
∴CD2+BC2=BD2,
∴∠BCD=90°,
这时Q与C点重合点Q坐标为Q(0,3),
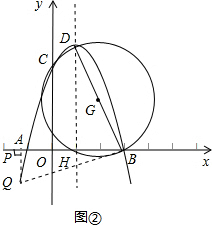 ②如图②,若∠DBQ为90°,作QP⊥x轴于P,DH⊥x轴于H
②如图②,若∠DBQ为90°,作QP⊥x轴于P,DH⊥x轴于H
可证Rt△DHB∽Rt△BPQ,
有
=
,
则点Q坐标(k,-k2+2k+3),
即
=
,
化简为2k2-3k-9=0,
即(k-3)(2k+3)=0,
解之为k=3或k=-
,
由k=-
得Q坐标:Q(-
,-
),
③若∠BDQ为90°,
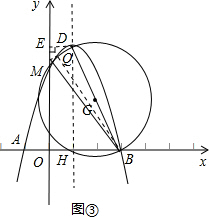 如图③,延长DQ交y轴于M,
如图③,延长DQ交y轴于M,
作DE⊥y轴于E,DH⊥x轴于H,
可证明△DEM∽△DHB,
即
=
,
则
=
,
得EM=
,
∵点M的坐标为(0,
),DM所在的直线方程为y=
x+
,
则y=
x+
与y=-x2+2x+3的解为x=
,
得交点坐标Q为(
,
),
即满足题意的Q点有三个,(0,3),(-
,-
),(
,
).
 解:(1)设抛物线的解析式为y=a(x+1)(x-3),
解:(1)设抛物线的解析式为y=a(x+1)(x-3),把(0,3)代入,
解得a=-1,
解析式为y=-x2+2x+3,
则点D的坐标为(1,4),
(2)设直线BC的解析式为y=kx+3,把B(3,0)代入,
解得k=-1,所以F(1,2),
∴DF=4-2=2,
△BCD的面积=
| 1 |
| 2 |
| 1 |
| 2 |
(3)①点C即在抛物线上,CD=
| 2 |
| 2 |
| 5 |
∵CD2+BC2=20,BD2=20,
∴CD2+BC2=BD2,
∴∠BCD=90°,
这时Q与C点重合点Q坐标为Q(0,3),
 ②如图②,若∠DBQ为90°,作QP⊥x轴于P,DH⊥x轴于H
②如图②,若∠DBQ为90°,作QP⊥x轴于P,DH⊥x轴于H可证Rt△DHB∽Rt△BPQ,
有
| DH |
| BP |
| HB |
| PQ |
则点Q坐标(k,-k2+2k+3),
即
| 4 |
| 3-k |
| 2 |
| k2-2k-3 |
化简为2k2-3k-9=0,
即(k-3)(2k+3)=0,
解之为k=3或k=-
| 3 |
| 2 |
由k=-
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
③若∠BDQ为90°,
 如图③,延长DQ交y轴于M,
如图③,延长DQ交y轴于M,作DE⊥y轴于E,DH⊥x轴于H,
可证明△DEM∽△DHB,
即
| DE |
| DH |
| EM |
| HB |
则
| 1 |
| 4 |
| EM |
| 2 |
得EM=
| 1 |
| 2 |
∵点M的坐标为(0,
| 7 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
则y=
| 1 |
| 2 |
| 7 |
| 2 |
| 1 |
| 2 |
得交点坐标Q为(
| 1 |
| 2 |
| 15 |
| 4 |
即满足题意的Q点有三个,(0,3),(-
| 3 |
| 2 |
| 9 |
| 4 |
| 1 |
| 2 |
| 15 |
| 4 |
点评:此题主要考查了二次函数解析式的确定、相似三角形的判定和应用、函数图象交点等知识,综合性强,考查学生分类讨论,数形结合的数学思想方法.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
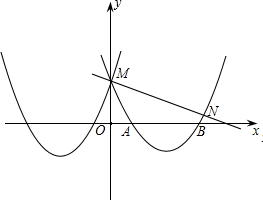 点M,与x轴交于点A和B.
点M,与x轴交于点A和B.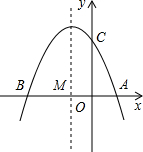 如图已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C.
如图已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C. 点M,与x轴交于点A和B.
点M,与x轴交于点A和B.