Question

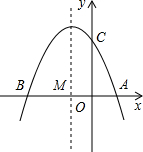如图已知抛物线y=ax²+bx+3（a≠0）与x轴交于点A（1，0）和点B（-3，0），与y轴交于点C．
（1）求抛物线的解析式；
（2）点D的坐标为（-2，0）．问：直线AC上是否存在点F，使得△ODF是等腰三角形？若存在，请直接写出所有符合条件的点F的坐标；若不存在，请说明理由．

Answer 1

分析：（1）将点A及点B的坐标代入可得出a、b的值，继而得出抛物线的解析式；
（2）先确定直线AC的解析式，若△ODF是等腰三角形，在本题中只有两种情况，①PD=PO，②OD=OP，分别确定点P的坐标即可．

解答：解：（1）将点A（1，0）和点B（-3，0）代入抛物线解析式可得：

a+b+3=0 9a-3b+3=0

，
解得：

a=-1 b=-2

，
故所求抛物线解析式为：y=-x²-2x+3．

（2）存在符合条件的点P，

设直线AC的解析式为y=kx+m，
将点A及点C的坐标代入可得：

k+m=0 m=3

，
解得：

k=-3 m=3

，
故直线AC的解析式为y=-3x+3，
①当PD=PO时，此时点P位于P₁的位置，很明显P₁的坐标为（-1，6）；
②当OD=OP时，此时点P的一个位置为P₂，
设P₂的坐标为（x，-3x+3），
∵OD=OP=2，
∴

x2+(-3x+3)2

=2，
解得：x₁=

18+ 31

10

，x₂=

18- 31

10

，
很明显此时P的坐标为（

18+ 31

10

，

-54- 31

10

）或（

18- 31

10

，

-54+3 31

10

）．
综上可得点P的坐标为（-1，6）或（

18+ 31

10

，

-54- 31

10

）或（

18- 31

10

，

-54+3 31

10

）．

点评：本题考查了二次函数的综合应用，第一问比较简单，利用待定系数法求解即可，难点在第二问，第二问关键是分类讨论，在求解点P的坐标的时候要求我们结合图形进行解答．