题目内容
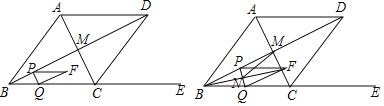
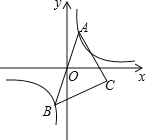
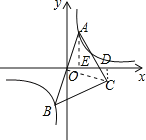
【题目】如图,已知点A是双曲线y=![]() 在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=![]() (k<0)上运动,则k的值是_____.
(k<0)上运动,则k的值是_____.
【答案】-1.
【解析】
连结OC,作CD⊥x轴于D,AE⊥x轴于E,设A点坐标为(a,![]() ),利用反比例函数的性质得到点A与点B关于原点对称,则OA=OB,再根据等腰直角三角形的性质得OC=OA,OC⊥OA,然后利用等角的余角相等可得到∠DCO=∠AOE,则根据“AAS”可判断△COD≌△OAE,所以OD=AE=
),利用反比例函数的性质得到点A与点B关于原点对称,则OA=OB,再根据等腰直角三角形的性质得OC=OA,OC⊥OA,然后利用等角的余角相等可得到∠DCO=∠AOE,则根据“AAS”可判断△COD≌△OAE,所以OD=AE=![]() ,CD=OE=a,于是C点坐标为(
,CD=OE=a,于是C点坐标为(![]() ,﹣a),最后根据反比例函数图象上点的坐标特征确定C点所在的函数图象解析式.
,﹣a),最后根据反比例函数图象上点的坐标特征确定C点所在的函数图象解析式.
解:连结OC,作CD⊥x轴于D,AE⊥x轴于E,
设A点坐标为(a,![]() ),
),
∵A点、B点是正比例函数图象与双曲线y=![]() 的交点,
的交点,
∴点A与点B关于原点对称,
∴OA=OB
∵△ABC为等腰直角三角形,
∴OC=OA,OC⊥OA,
∴∠DOC+∠AOE=90°,
∵∠DOC+∠DCO=90°,
∴∠DCO=∠AOE,
在△COD和△OAE中,
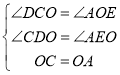 ,
,
∴△COD≌△OAE,
∴OD=AE,CD=OE,
∴点C的坐标为(![]() ,﹣a),
,﹣a),
![]() ×(﹣a)=﹣1,
×(﹣a)=﹣1,
∴k=﹣1.
故答案为:﹣1.

 阅读快车系列答案
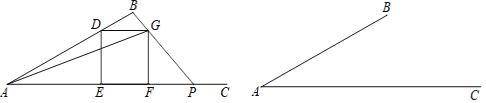
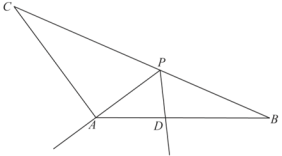
阅读快车系列答案【题目】如图,在钝角![]() 中,点
中,点![]() 为
为![]() 上的一个动点,连接
上的一个动点,连接![]() ,将射线
,将射线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,交线段
,交线段![]() 于点
于点![]() . 已知∠C=30°,CA=2
. 已知∠C=30°,CA=2![]() cm,BC=7cm,设B,P两点间的距离为xcm,A,D两点间的距离ycm.
cm,BC=7cm,设B,P两点间的距离为xcm,A,D两点间的距离ycm.
小牧根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.下面是小牧探究的过程,请补充完整:
的变化而变化的规律进行了探究.下面是小牧探究的过程,请补充完整:
(1)根据图形.可以判断此函数自变量X的取值范围是 ;
(2)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
| 0.51 | 1.02 | 1.91 | 3.47 | 3 | 4.16 | 4.47 |
|
|
| 3.97 | 3.22 | 2.42 | 1.66 | a | 2.02 | 2.50 |
|
通过测量。可以得到a的值为 ;
(3)在平而直角坐标系xOy中.描出上表中以各对对应值为坐标的点,画出该函数的图象;
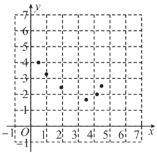
(4)结合画出的函数图象,解决问题:当AD=3.5cm时,BP的长度约为 cm.