题目内容
【题目】甲、乙两站相距336千米,一列慢车从甲站开出,每小时行驶72千米,一列快车从乙站开出,每小时行驶96千米.
(1)若两车同时相向而行,则几小时后相遇?几小时后相距84千米?
(2)若两车同时反向而行,则几小时后相距672千米?
【答案】(1)2小时后相遇 1.5小时或2.5小时后相距84千米;
(2)2小时后相距672千米.
【解析】试题分析:
(1) 下面分析第一个问题,根据题意可画出如下线段示意图.
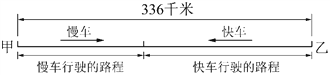
观察上图可以发现,当两车相遇时,慢车行驶的路程与快车行驶的路程之和应等于两车站之间的距离336千米. 根据“路程等于速度乘以时间”,若设两车x小时后相遇,则慢车行驶的路程与快车行驶的路程均可用x表示出来,再根据上述等量关系可列出方程并求解.
下面分析第二个问题.
由于两站之间的距离为336千米,所以在两车同时相向而行的条件下,两车相距84千米的情况可能发生在两车相遇之前,也可能发生在两车相遇之后. 因此,该问题应该分情况求解.
① 若该情况发生在两车相遇之前,根据题意可画出如下线段示意图.
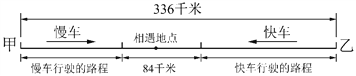
观察上图可以发现,若该情况发生在两车相遇之前,慢车行驶的路程与快车行驶的路程之和再加上84千米应等于两车站之间的距离336千米. 根据这一等量关系可以列出方程并求解.
② 当该情况发生在两车相遇之后,根据题意可画出如下线段示意图.
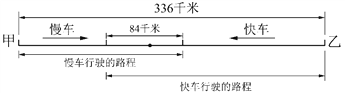
观察上图可以发现,若该情况发生在两车相遇之后,慢车行驶的路程与快车行驶的路程之和应再减去84千米才等于两车站之间的距离336千米. 根据这一等量关系可以列出方程并求解.
(2) 根据题意可画出如下线段示意图.

观察上图可以发现,若两车同时反向而行,慢车行驶的路程与快车行驶的路程之和再加上336千米应等于两车之间的距离672千米. 根据这一等量关系可以列出方程并求解.
试题解析:
(1) 设两车同时相向而行,x小时后相遇.
根据题意,得
72x+96x=336
合并同类项,得 168x=336,
系数化为1,得 x=2.
故两车同时相向而行2小时后相遇.
在两车同时相向而行的条件下,两车相距84千米的情况应该分为在两车相遇之前以及在两车相遇之后两种情况求解.
①在两车相遇之前,设y小时后两车相距84千米.
72y+96y+84=336
合并同类项,得 168y=252,
系数化为1,得 y=1.5.
因为两车同时相向而行2小时后相遇,y=1.5<2,所以y=1.5是合理的.
②在两车相遇之后,设y小时后两车相距84千米.
72y+96y-84=336
合并同类项,得 168y=420,
系数化为1,得 y=2.5.
因为两车同时相向而行2小时后相遇,y=2.5>2,所以y=2.5是合理的.
答:两车同时相向而行,2小时后相遇;两车从各自车站开出1.5小时或2.5小时后相距84千米.
(2) 设两车同时反向而行,x小时后相距672千米.
根据题意,得
72x+96x+336=672
移项,得 72x+96x=672-336,
合并同类项,得 168x=336,
系数化为1,得 x=2.
答:两车同时反向而行,2小时后相距672千米.