Question

【题目】如图，直线y=2x+3与x轴相交于点A，与y轴相交于点B.

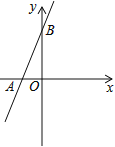
（1）求A，B两点的坐标；

（2）过B点作直线BP与x轴相交于P，且使OP=2OA， 求直线BP的解析式.

Answer 1

【答案】（1）（-，0）；（0，3）；（2）y=x+3或y=-x+3．

【解析】试题分析：（1）根据坐标轴上点的坐标特征确定A点和B点坐标；

（2）由OA=，OP=2OA得到OP=3，分类讨论：当点P在x轴正半轴上时，则P点坐标为（3，0）；当点P在x轴负半轴上时，则P点坐标为（-3，0），然后根据待定系数法求两种情况下的直线解析式．

试题解析：（1）把x=0代入y=2x+3，得y═3，

则B点坐标为（0，3）；

把y=0代入y=2x+3，得0=2x+3，

解得x=-，

则A点坐标为（-，0）；

（2）∵OA=，

∴OP=2OA=3，

当点P在x轴正半轴上时，则P点坐标为（3，0），

设直线BP的解析式为：y=kx+b，

把P（3，0），B（0，3）代入得

解得：

∴直线BP的解析式为：y=-x+3；

当点P在x轴负半轴上时，则P点坐标为（-3，0），

设直线BP的解析式为y=kx+b，

把P（-3，0），B（0，3）代入得

解得:k=1，b=3

所以直线BP的解析式为：y=x+3；

综上所述，直线BP的解析式为y=x+3或y=-x+3．