题目内容
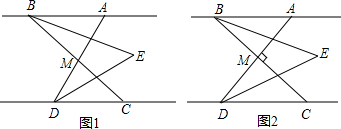
如图，△ABC中，∠A=62°，作CD∥AB，点E在AC上，点F在△ABC内，且∠FEC=62°，连接BF．请你探索∠1、∠2、∠F三个角之间的关系，并给出证明．
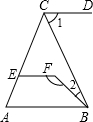
三个角之间关系为：∠1+∠F+∠2=180°．理由如下：（2分）
∵CD∥AB，
∴∠1=∠CBA=∠2+∠FBA，（两直线平行，内错角相等）
即∠FBA=∠1-∠2①，（4分）
又∵∠A=∠FEC=62°，
∴EF∥AB（同位角相等，两直线平行），（6分）
∴∠F+∠FBA=180°，（两直线平行，同旁内角互补）
即∠FBA=180°-∠F②，（8分）
由①、②得∠1-∠2=180°-∠F，
即∠1+∠F-∠2=180°．（10分）
∵CD∥AB，
∴∠1=∠CBA=∠2+∠FBA，（两直线平行，内错角相等）
即∠FBA=∠1-∠2①，（4分）
又∵∠A=∠FEC=62°，
∴EF∥AB（同位角相等，两直线平行），（6分）
∴∠F+∠FBA=180°，（两直线平行，同旁内角互补）
即∠FBA=180°-∠F②，（8分）
由①、②得∠1-∠2=180°-∠F，
即∠1+∠F-∠2=180°．（10分）
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
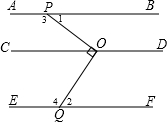始终在∠POQ的内部．
