题目内容
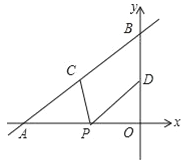
【题目】如图，直线
与x轴、y轴分别交于点A和点B，点C、D分别为线段AB、OB的中点，点P为OA上一动点，PC+PD值最小时点P的坐标为（ ）
A．（﹣3，0） B．（﹣6，0） C．（
，0） D．（
，0）
【答案】C．
【解析】
试题分析：作点D关于x轴的对称点D′，连接CD′交x轴于点P，此时PC+PD值最小，如图所示．
令
中x=0，则y=4，∴点B的坐标为（0，4）；
令中y=0，则
，解得：x=﹣6，∴点A的坐标为（﹣6，0）．
∵点C、D分别为线段AB、OB的中点，∴点C（﹣3，2），点D（0，2）．
∵点D′和点D关于x轴对称，∴点D′的坐标为（0，﹣2）．
设直线CD′的解析式为y=kx+b，∵直线CD′过点C（﹣3，2），D′（0，﹣2），∴有
，解得：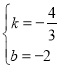
，∴直线CD′的解析式为
．
令中y=0，则
，解得：x=
，∴点P的坐标为（，0）．
故选C．
练习册系列答案
黎明文化寒假作业系列答案
相关题目
