ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΩΈ±ΨΆΊ’Ι
Ψ…÷Σ–¬“βΘΚ
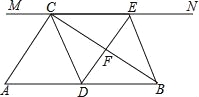
Έ“Ο«»ί“Ή÷ΛΟςΘ§»ΐΫ«–ΈΒΡ“ΜΗωΆβΫ«Β»”Ύ”κΥϋ≤ΜœύΝΎΒΡΝΫΗωΡΎΫ«ΒΡΚΆΘ°Ρ«Ο¥Θ§»ΐΫ«–ΈΒΡ“ΜΗωΡΎΫ«”κΥϋ≤ΜœύΝΎΒΡΝΫΗωΆβΫ«ΒΡΚΆ÷°Φδ¥φ‘Ύ‘θ―υΒΡ ΐΝΩΙΊœΒΡΊΘΩ
1Θ°≥Δ ‘ΧΫΨΩΘΚ
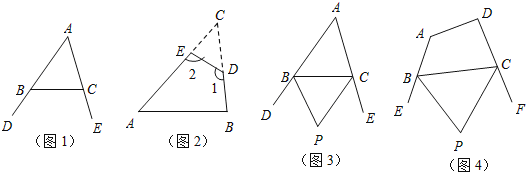
Θ®1Θ©»γΆΦ1Θ§ΓœDBC”κΓœECBΖ÷±πΈΣΓςABCΒΡΝΫΗωΆβΫ«Θ§ ‘ΧΫΨΩΓœA”κΓœDBC+ΓœECB÷°Φδ¥φ‘Ύ‘θ―υΒΡ ΐΝΩΙΊœΒΘΩΈΣ ≤Ο¥ΘΩ
2Θ°≥θ≤Ϋ”Π”ΟΘΚ
Θ®2Θ©»γΆΦ2Θ§‘ΎΓςABC÷ΫΤ§÷–Φτ»ΞΓςCEDΘ§ΒΟΒΫΥΡ±Ώ–ΈABDEΘ§Γœ1=130ΓψΘ§‘ρΓœ2-ΓœC= ΘΜ
Θ®3Θ©–ΓΟςΝΣœκΒΫΝΥ‘χΨ≠ΫβΨωΒΡ“ΜΗωΈ ΧβΘΚ»γΆΦ3Θ§‘ΎΓςABC÷–Θ§BPΓΔCPΖ÷±πΤΫΖ÷ΆβΫ«ΓœDBCΓΔΓœECBΘ§ΓœP”κΓœA”–ΚΈ ΐΝΩΙΊœΒΘΩ«κάϊ”Ο…œΟφΒΡΫα¬έ÷±Ϋ”–¥≥ω¥πΑΗ Θ°
3ΆΊ’ΙΧα…ΐΘΚ
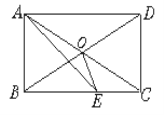
Θ®4Θ©»γΆΦ4Θ§‘ΎΥΡ±Ώ–ΈABCD÷–Θ§BPΓΔCPΖ÷±πΤΫΖ÷ΆβΫ«ΓœEBCΓΔΓœFCBΘ§ΓœP”κΓœAΓΔΓœD”–ΚΈ ΐΝΩΙΊœΒΘΩΈΣ ≤Ο¥ΘΩΘ®»τ–η“Σάϊ”Ο…œΟφΒΡΫα¬έΥΒΟςΘ§Ω…÷±Ϋ” Ι”ΟΘ§≤Μ–ηΥΒΟςάμ”…Θ©
ΓΨ¥πΑΗΓΩΘ®1Θ©ΓœDBC+ΓœECB=180Γψ+ΓœAΘΜΘ®2Θ©50ΓψΘΜΘ®3Θ©ΓœP=90Γψ-![]() ΓœAΘΜΘ®4Θ©ΓœBAD+ΓœCDA=360Γψ-2ΓœPΘ°
ΓœAΘΜΘ®4Θ©ΓœBAD+ΓœCDA=360Γψ-2ΓœPΘ°
ΓΨΫβΈωΓΩ
‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΗυΨί»ΐΫ«–ΈΒΡ“ΜΗωΆβΫ«Β»”Ύ”κΥϋ≤ΜœύΝΎΒΡΝΫΗωΡΎΫ«ΒΡΚΆ±μ Ψ≥ωΓœDBC+ΓœECBΘ§‘Όάϊ”Ο»ΐΫ«–ΈΡΎΫ«ΚΆΕ®άμ’ϊάμΦ¥Ω…ΒΟΫβΘΜ
Θ®2Θ©ΗυΨίΘ®1Θ©ΒΡΫα¬έ’ϊάμΦΤΥψΦ¥Ω…ΒΟΫβΘΜ
Θ®3Θ©±μ Ψ≥ωΓœDBC+ΓœECBΘ§‘ΌΗυΨίΫ«ΤΫΖ÷œΏΒΡΕ®“ε«σ≥ωΓœPBC+ΓœPCBΘ§»ΜΚσάϊ”Ο»ΐΫ«–ΈΡΎΫ«ΚΆΕ®άμΝ– Ϋ’ϊάμΦ¥Ω…ΒΟΫβΘΜ
Θ®4Θ©―”≥ΛBAΓΔCDœύΫΜ”ΎΒψQΘ§œ»”ΟΓœQ±μ Ψ≥ωΓœPΘ§‘Ό”ΟΘ®1Θ©ΒΡΫα¬έ’ϊάμΦ¥Ω…ΒΟΫβΘ°
‘ΧβΫβΈωΘΚΘ®1Θ©ΓœDBC+ΓœECB
=180Γψ-ΓœABC+180Γψ-ΓœACB
=360Γψ-Θ®ΓœABC+ΓœACBΘ©
=360Γψ-Θ®180Γψ-ΓœAΘ©
=180Γψ+ΓœAΘΜ
Θ®2Θ©ΓΏΓœ1+Γœ2=Γœ180Γψ+ΓœCΘ§
Γύ130Γψ+Γœ2=180Γψ+ΓœCΘ§
ΓύΓœ2-ΓœC=50ΓψΘΜ
Θ®3Θ©ΓœDBC+ΓœECB=180Γψ+ΓœAΘ§
ΓΏBPΓΔCPΖ÷±πΤΫΖ÷ΆβΫ«ΓœDBCΓΔΓœECBΘ§
ΓύΓœPBC+ΓœPCB=![]() Θ®ΓœDBC+ΓœECBΘ©=
Θ®ΓœDBC+ΓœECBΘ©=![]() Θ®180Γψ+ΓœAΘ©Θ§
Θ®180Γψ+ΓœAΘ©Θ§
‘ΎΓςPBC÷–Θ§ΓœP=180Γψ-![]() Θ®180Γψ+ΓœAΘ©=90Γψ-
Θ®180Γψ+ΓœAΘ©=90Γψ-![]() ΓœAΘΜ
ΓœAΘΜ
Φ¥ΓœP=90Γψ-![]() ΓœAΘΜ
ΓœAΘΜ
Θ®4Θ©―”≥ΛBAΓΔCD”ΎQΘ§
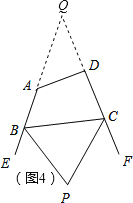
‘ρΓœP=90Γψ-![]() ΓœQΘ§
ΓœQΘ§
ΓύΓœQ=180Γψ-2ΓœPΘ§
ΓύΓœBAD+ΓœCDA=180Γψ+ΓœQΘ§
=180Γψ+180Γψ-2ΓœPΘ§
=360Γψ-2ΓœPΘ°

 ΩΣ–ΡΩλά÷ΦΌΤΎΉς“Β νΦΌΉς“ΒΈςΑ≤≥ωΑφ…γœΒΝ–¥πΑΗ
ΩΣ–ΡΩλά÷ΦΌΤΎΉς“Β νΦΌΉς“ΒΈςΑ≤≥ωΑφ…γœΒΝ–¥πΑΗ ΟϊΧβ―ΒΝΖœΒΝ–¥πΑΗ
ΟϊΧβ―ΒΝΖœΒΝ–¥πΑΗ