题目内容
（2011•徐汇区一模）抛物线y=-x2+bx+c与x轴交于A（1，0），B（-3，0）两点，则二次函数解析式是 ．
【答案】分析：由于抛物线y=-x2+bx+c与x轴交于A（1，0），B（-3，0）两点，那么可以得到方程-x2+bx+c=0的两根为x=1或x=-3，然后利用根与系数即可确定b、c的值．
解答：解：∵抛物线y=-x2+bx+c与x轴交于A（1，0），B（-3，0）两点，
∴方程-x2+bx+c=0的两根为x=1或x=-3，
∴1+（-3）=b，
1×（-3）=-c，
∴b=-2，c=3，
∴二次函数解析式是y=-x2-2x+3．
点评：此题主要考查了利用抛物线与x轴的交点坐标确定函数解析式，解题的关键是利用待定系数法得到关于b、c的方程，解方程即可解决问题．
解答：解：∵抛物线y=-x2+bx+c与x轴交于A（1，0），B（-3，0）两点，
∴方程-x2+bx+c=0的两根为x=1或x=-3，
∴1+（-3）=b，
1×（-3）=-c，
∴b=-2，c=3，
∴二次函数解析式是y=-x2-2x+3．
点评：此题主要考查了利用抛物线与x轴的交点坐标确定函数解析式，解题的关键是利用待定系数法得到关于b、c的方程，解方程即可解决问题．
练习册系列答案
全能测控一本好卷系列答案
相关题目
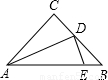
与x轴相交于A、B，与y轴相交于点C，过点C作CD∥x轴，交抛物线点D．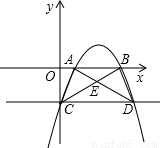
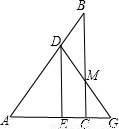
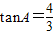，E为线AC上一点（不与A、C重合），过点E作EDACED⊥AC交线段AB于点D，将△ADE沿着直线DE翻折，A的对应点G落在射线AC上，线段DG与线段BC交于点M．
