题目内容
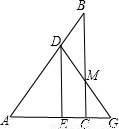
（2011•徐汇区一模）如图，在△ABC中，AC=BC=2，∠C=90°，点D为腰BC中点，点E在底边AB上，且DE⊥AD，则BE的长为 ．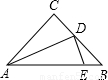
【答案】分析：先根据已知条件，利用勾股定理分别求出AB、AD的长，再根据射影定理求出AE的长，然后用AB减去AE即可得EB．
解答：
解：过D点作DH⊥AB，垂足为H，
∵在△ABC中，AC=BC=2，∠C=90°，
∴AB=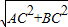
=2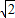
．
∵点D为腰BC中点，
∴AD=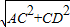
=
，
∵DE⊥AD，∠B=45°
∴DH=HB=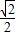
∴AD2=AH•AE，
∴AE=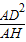
=
=
，
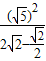EB=AB-AE=2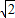
-
=
．
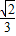故答案为：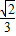
．
点评：此题主要考查学生对勾股定理的理解和掌握，解答关键是过D点作DH⊥AB，求出AE的长，这是此题的突破点，此题有点难度，属于中档题．
解答：
解：过D点作DH⊥AB，垂足为H，∵在△ABC中，AC=BC=2，∠C=90°，
∴AB=
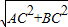=2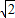．∵点D为腰BC中点，
∴AD=
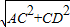=，∵DE⊥AD，∠B=45°
∴DH=HB=
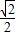
∴AD2=AH•AE，
∴AE=
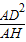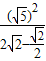==，EB=AB-AE=2
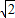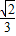-=．故答案为：
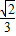．点评：此题主要考查学生对勾股定理的理解和掌握，解答关键是过D点作DH⊥AB，求出AE的长，这是此题的突破点，此题有点难度，属于中档题．
练习册系列答案
相关题目
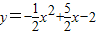与x轴相交于A、B，与y轴相交于点C，过点C作CD∥x轴，交抛物线点D．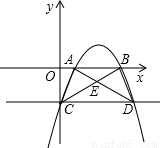
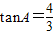，E为线AC上一点（不与A、C重合），过点E作EDACED⊥AC交线段AB于点D，将△ADE沿着直线DE翻折，A的对应点G落在射线AC上，线段DG与线段BC交于点M．