题目内容
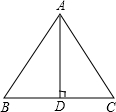 已知:如图所示,等边三角形ABC的边长是6cm.求:(1)高AD的长;(2)△ABC的面积S△ABC.
已知:如图所示,等边三角形ABC的边长是6cm.求:(1)高AD的长;(2)△ABC的面积S△ABC.
解:(1)∵AD⊥BC,
∴BD=CD= ×6=3cm,
×6=3cm,
∴AD=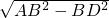 =
=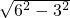 =3
=3 cm;
cm;
(2)S△ABC= ×BC•AD=
×BC•AD= ×6×3
×6×3 =9
=9 cm2.
cm2.
分析:(1)根据等腰三角形三线合一求出BD的长度是3cm,再利用勾股定理即可求出BD的长度;
(2)根据三角形的面积公式S= ah,代入数据计算即可.
ah,代入数据计算即可.
点评:本题主要利用等边三角形是特殊的等腰三角形,等腰三角形“三线合一”,勾股定理,三角形的面积公式,熟练掌握定理和公式是解题的关键.
∴BD=CD=
 ×6=3cm,
×6=3cm,∴AD=
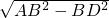 =
=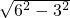 =3
=3 cm;
cm;(2)S△ABC=
 ×BC•AD=
×BC•AD= ×6×3
×6×3 =9
=9 cm2.
cm2.分析:(1)根据等腰三角形三线合一求出BD的长度是3cm,再利用勾股定理即可求出BD的长度;
(2)根据三角形的面积公式S=
 ah,代入数据计算即可.
ah,代入数据计算即可.点评:本题主要利用等边三角形是特殊的等腰三角形,等腰三角形“三线合一”,勾股定理,三角形的面积公式,熟练掌握定理和公式是解题的关键.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
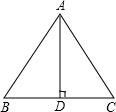 已知:如图所示,等边三角形ABC的边长是6cm.求:(1)高AD的长;(2)△ABC的面积S△ABC.
已知:如图所示,等边三角形ABC的边长是6cm.求:(1)高AD的长;(2)△ABC的面积S△ABC.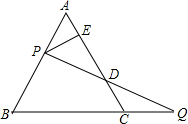 已知:如图所示,等边三角形ABC的边长为2,点P和Q分别从A和C两点同时出发,做匀速运动,且它们的速度相同.点P沿射线AB运动,点Q沿边BC的延长线运动,设PQ与直线AC相交于点D,作PE⊥AC于E,当P和Q运动时,线段DE的长是否改变?证明你的结论.
已知:如图所示,等边三角形ABC的边长为2,点P和Q分别从A和C两点同时出发,做匀速运动,且它们的速度相同.点P沿射线AB运动,点Q沿边BC的延长线运动,设PQ与直线AC相交于点D,作PE⊥AC于E,当P和Q运动时,线段DE的长是否改变?证明你的结论. 已知:如图所示,点C在线段AB上,分别以AC、BC为一边作为等边△ACM和等边△BCN,连接AN、BM.
已知:如图所示,点C在线段AB上,分别以AC、BC为一边作为等边△ACM和等边△BCN,连接AN、BM.